Artiruno: A free-software tool for multi-criteria decision-making with verbal decision analysis
Created 21 Apr 2023 • Last modified 6 Jan 2026
Verbal decision analysis (VDA) is a family of methods for multi-criteria decision analysis that require no numerical judgments from the agent. Although many such methods have been developed, they share the potential issue of asking the agent many more questions than necessary, particularly under multilevel approaches. Furthermore, whether VDA improves decisions, compared to no intervention, has yet to be investigated empirically. I introduce a new VDA method, Artiruno, with a freely licensed implementation in Python. Artiruno makes inferences mid-interview so as to require minimal input from the agent, while using a multilevel scheme that allows it to ask complex questions when necessary. Inferences are facilitated by an axiom allowing comparisons to be partitioned across groups of criteria. Artiruno's performance in a variety of simple and complex scenarios can be verified with automated software tests. For an empirical test, I conducted an experiment in which 107 people from an Internet subject pool considered an important decision they faced in their own lives, and were randomly assigned to use Artiruno or to receive no intervention. These subjects proved mostly able to use Artiruno, and they found it helpful, but Artiruno seemed to have little influence on their decisions or outcomes.
This paper was published as:
Arfer, K. B. (2024). Artiruno: A free-software tool for multi-criteria decision-making with verbal decision analysis. Journal of Multi-Criteria Decision Analysis, 31. doi:10.1002/mcda.1827.
The official Wiley PDF has only minor differences from this the original document.
Acknowledgments
Thanks to Akos Szekely for help editing the subject instructions for the empirical study, and to Kelly A. Matula for help assessing subjects' written criteria and alternatives.
Introduction
Extant methods
Most methods for multi-criteria decision analysis (MCDA) require the agent to make numerical judgments. For example, in methods based on multiattribute utility or approximations thereof, such as simple multiattribute rating theory (SMART; Edwards, 1977), agents rate each criterion's importance with integers increasing from 10, and then they quantify the level of each option on each criterion using physical units or an abstract 0-to-100 scale. Or in the Analytic Hierarchy Process (AHP), agents rate each pair of alternatives on each criterion, as well as each pair of criteria, on 1-to-9 scales (Saaty & Vargas, 2012). The numbers are related to each other either with functions chosen by the agent or by standard functions, such as, in the case of SMART, linear preference from the lowest plausible value to the highest plausible value. Numerical judgments and functions to operate on them are a great help to the development of methods, which can then proceed with quantitative operations. The trouble is that the outcome can of course be sensitive to agents' numerical judgments, which can be imprecise or inaccurate, particularly when rather abstract, such as importance ratings.
Outranking methods represent an alternative or supplement to more utility-oriented MCDA methods. In outranking, the goal is to find ordinal relations among options. Ordinal relations, as opposed to cardinal relations, suffice for many real-world decisions (such as hiring from a pool of applicants to fill a limited number of jobs) while potentially demanding less rich quantitative judgments from agents. A drawback is that the method may deem some options incomparable, making the result only a partial order. One example of an outranking method is Visual PROMETHEE (Mareschal, 2013), which allows criteria to be continuous or ordinal, and produces ordinal results about the alternatives. While less numerical, outranking is not necessarily a complete escape from numerical judgments. In the case of Visual PROMETHEE, the criteria must be weighted numerically even if all of them are ordinal.
Verbal decision analysis (VDA; Moshkovich, Mechitov, & Olson, 2016) was introduced by Larichev and Moshkovich (1997) as an approach to outranking that requires no numerical judgments at all. This approach was inspired by research in experimental psychology about what kinds of cognitive operations people can perform most reliably (Larichev, Polyakov, & Nikiforov, 1987). With a VDA method, such as ZAPROS (Larichev & Moshkovich, 1995; Larichev, 2001), the agent defines all criteria ordinally and then makes judgments about the relative appeal of hypothetical alternatives. From these judgments and a few conservative assumptions about the ordinal structure of preferences, VDA can infer an order for the real alternatives. The key idea is to present hypothetical decisions to the agent that are easier to make than the real decision, because fewer criteria are allowed to vary, yet are informative about the comparisons involved in the real decision. VDA is a natural fit for complex real-world decisions in which criteria are difficult to measure and weight, such as a hiring decision that must take into account subjective judgments of candidates' qualities. Further developments of VDA methods and software since the earliest iterations of ZAPROS include UniComBOS (Ashikhmin & Furems, 2005), ORCON_Z (Moshkovich & Mechitov, 2018), and ORCLASSWEB (Barbosa, Pinheiro, Silveira, & Filho, 2019). DEX (Bohanec & Rajkovič, 1990) is an example of a method that, while not construed as a form of VDA, uses VDA-like qualitative criterion scales.
A limitation of the extant VDA methods is that the questions they ask the agent in order to come to their recommendations are insensitive to the specific decision that needs to be made. In ZAPROS, for example, the agent must make a judgment about every pair of criterion levels, whether or not that judgment is necessary for the conclusion. This exhaustiveness is an inefficient use of the agent's attention, possibly reducing accuracy or user acceptability, and makes large numbers of criteria or levels impractical. If the method allows comparing more than two criteria levels at once, in order to alleviate the incomparability issues that outranking methods are prone to, then the agent needs to make even more judgments. Furthermore, this practice of judging criterion levels in isolation, outside the context of fully defined hypothetical alternatives, may undermine VDA's goal of focusing on psychologically realistic judgments.
Another potential problem with VDA, as with many MCDA methods, is a lack of direct empirical investigation of how effective the methods are in improving decisions. The theory is rich, as are examples of real-world use, but one may still ask whether using VDA results in better decisions than not using it—even in a weak sense of decision quality that only measures how satisfied people are with their decisions.
Artiruno
In the present article, I describe a new VDA method that I call "Artiruno". Artiruno's most important innovation in VDA methdology is its tactical selection of questions. The agent can declare that all he requires is to find the n best alternatives (typically the single best), and Artiruno will make inferences mid-interview to ask the questions most relevant to the goal. Even if the agent declares a goal of comparability between all alternatives, Artiruno can still benefit from online inference. Questions whose answers are implied by previous answers are omitted entirely, making it impossible for the agent to provide inconsistent answers. Intelligent selection of questions lowers the decision-making burden on the agent and makes large item spaces feasible: a problem with 10 criteria that each have 10 levels need not require asking billions of questions, or holding in memory a data structure with billions of items. Such selectiveness is especially helpful because Artiruno is multilevel like UniComBOS, in the sense that it can vary two or more criteria at once in its questions it asks of the agent.
To check that intended theoretical guarantees are met and efficiency goals are maintained, Artiruno includes a test suite. Automated tests ensure that simple features of Artiruno (e.g., trivial ordinal inferences) as well as complex features (e.g., inference of preferences defined by a randomly generated additive utility function) are designed and implemented correctly.
To examine how helpful Artiruno is for real-life decision-making, I subject it to an empirical test that MCDA methods (especially VDA) are rarely given. Namely, I compare decision outcomes and user satisfaction when decision-makers—non-experts, in fact—were randomly assigned to use Artiruno or to receive no special help. Randomized controlled trials such as this are generally seen as essential for evaluating medical and psychological interventions because they allow for straightforward causal inferences (Sibbald & Roland, 1998), but they appear underused in research on MCDA and more generally decision aid. The subjects of this empirical study considered decision scenarios they faced in their own lives, leading Artiruno to be tested in a variety of domains.
Design and implementation
Theory
Like all VDA methods, Artiruno represents a decision scenario using finitely many criteria and items. The criteria, representing dimensions on which an item may be judged, are finite tuples of levels or opaque values. In a decision between job offers, for example, a criterion might be "Salary", with the levels "Low", "Medium", and "High". Levels are ordered such that each level is strictly better than (i.e., preferred to) the one before it, so a job with "Medium" salary is better than a job with "Low" salary, all other things being equal. Essentially, this is an assumption of preferential independence. On the other hand, no order is assumed between criteria. The items, representing imaginable options, are the Cartesian product of all the criteria, while a subset of the items, the alternatives, represent the specific options that the agent can decide between. Thus, each alternative has exactly one value for each criterion, which is a level of that criterion, and the agent's preferences regarding an item are assumed to be completely determined by its values for the criteria. The job-offers scenario might look like this:
- Criteria
- (A) Salary: "Low", "Medium", "High"
- (B) Location: "Far from home", "Ideal"
- (C) Training opportunities: "Low", "High"
- (D) Promotion opportunities: "Low", "High"
- Alternatives
- (a) Dewey, Cheatem & Howe
- Salary: (A3) "High"
- Location: (B2) "Ideal"
- Training opportunities: (C1) "Low"
- Promotion opportunities: (D1) "Low"
- (b) MicroCo.
- Salary: (A2) "Medium"
- Location: (B1) "Far from home"
- Training opportunities: (C2) "High"
- Promotion opportunities: (D2) "High"
- (a) Dewey, Cheatem & Howe
The agent's preferences among the items are represented as a preorder, which is defined as a reflexive and transitive binary relation. The relation a ≤ b for any items a and b means that a is no better than b; that is, a is worse than or equally as good as b. Notice that a preorder allows the agent to be indifferent between two items, denoted a ≈ b, meaning a ≤ b and a ≥ b even though a need not equal b. Preorders also allow a pair of items to be incomparable. However, incomparability represents Artiruno's ignorance of the agent's preference regarding a pair of items. It is assumed that the agent's true preferences are a total preorder, and Artiruno asks the agent questions towards the goal of replacing incomparability with one of the three relations a < b, a > b, or a ≈ b.
To extend the inferences Artiruno can make, one more assumption is included: the rule of segmentwise dominance. Intuitively, the rule of segmentwise dominance says that if the comparison of two items can be broken down into several comparisons on subsets of the criteria ("segments"), all those comparisons agree, and all the segments together cover all the criteria, then we can infer a relation between the original two items.
- In the simple case, the rule of dominance states that for any items a = (aA, aB, aC, …) and b = (bA, bB, bC, …), if ai ≤ bi for all i and ai < bi for some i, then a < b. We say that b dominates a, or if an item dominates all other items in a set, that it is a dominator of that set.
- The rule of segmentwise dominance generalizes dominance as follows. For each item p and each subset σ of the criteria, let R(σ, p) be the item that has the best value on all criteria except possibly the criteria in σ, for which it has the criterion values of p. In other words, R(σ, p) can only deviate from the best constructible item on σ, and the values for σ are taken from p. Then let a and b be distinct items, and let {α1, α2, …, αm} and {β1, β2, …, βm} be partitions of the criteria (which need not be distinct, and notice that both partitions have the same number of sets, m, although the cardinalities of those sets may vary). Segmentwise dominance applies when R(αi, a) ≤ R(βi, b) for all i. If R(αi, a) < R(βi, b) for some i, then a < b; otherwise, a ≈ b.
For an example of segmentwise dominance, consider the job-offers scenario laid out above. Let a be Dewey, Cheatem & Howe and b be MicroCo. Representing the criteria as {A, B, C, D} and their levels as {A1, A2, A3, B1, B2, C1, C2, D1, D2}, let α1 = {A, B, D} and α2 = {C} while β1 = {A, C, D} and β2 = {B}. Suppose we know from previous responses the agent has given that R(α1, a) = (A3, B2, C2, D1) < (A2, B2, C2, D2) = R(β1, b), while R(α2, a) = (A3, B2, C1, D2) < (A3, B1, C2, D2) = R(β2, b). Then segmentwise dominance applies, and we conclude that a < b.
Artiruno is intended to be able to find the single best item in a set of alternatives, or more generally the best n. For this purpose, we define the top-n subset of a preordered set as a generalization of the notion of a maximum, distinct from the notion of a maximal element. Given a preordered set X, the top-n subset is the set of all elements x ∈ X such that
- x is comparable to every element of X, and
- there are at most n − 1 distinct elements a ∈ X with a > x.
In the case of a total order, the top-1 subset is simply the singleton of the maximum of S, and the top-n subset has cardinality n so long as n ≤ |S|. For preorders, however, the complication of indifference means that the top-n subset can be of any cardinality {0, 1, …, |S|}.
Software
I distinguish Artiruno from previous VDA software by making it permanently available (on GitHub at https://github.com/Kodiologist/Artiruno, or on the Internet Archive at http://web.archive.org/web/20230924/https://codeload.github.com/Kodiologist/Artiruno/tar.gz/refs/tags/v0.4.2) under a free license, the GNU GPL version 3 or later. Artiruno is free software in the sense of the Free Software Foundation (2008): it may be freely copied, studied, and modified without technical or legal restrictions, contributing to the larger goal of open science (Woelfle, Olliaro, & Todd, 2011). Artiruno is written in Python, a popular programming language in science (Millman & Aivazis, 2011) described as a "lingua franca" for scientific computing (Thomas & Christensen, 2014) and computer-science education (Hunt, 2014). As a concise, readable, and easy-to-learn language, Python is well suited to this role. Other Python libraries for MCDA include pymcdm (Kizielewicz, Shekhovtsov, & Sałabun, 2023) and AHPy.
An additional strength of Artiruno's implementation is its web interface. At http://arfer.net/projects/artiruno/webi, anyone can quickly try out Artiruno (on a preprovided example scenario, or one of their own design) using only a web browser.
Operation
This section describes the operation of Artiruno in overview, while referring to particular modules and objects in the code where full details may be found.
One core component of Artiruno is PreorderedSet, a generic class of data structure for representing a set equipped with a preorder. It can contain many types of objects, such as numbers or strings; for VDA, it contains tuples to represent items that the agent may consider. Each pair of elements in the set has one of four corresponding relations: strictly less than (LT), strictly greater than (GT), indifference (EQ), or incomparability (IC). The class supports two important mutating operations. The method add puts a new object in the set, making it initially incomparable to all other objects. The method learn takes two objects already in the set and a relation, and updates the preorder with a modification of Warshall's algorithm of transitive closure (Ingerman, 1962) to reflect this new fact, adding all further relations that can be inferred by transitivity. If the new fact leads to a contradiction, the exception ContradictionError is raised; thus, in the absence of exceptions, the user is assured of a consistent preorder. Finally, PreorderedSet can generate a graph of all relations that can be displayed with Graphviz (Gansner & North, 2000) for easy visualization of complex relational networks (see e.g. Figure 2).
The key function for VDA is vda, which takes lists of criteria and alternatives as arguments. It begins by checking that these are well-formed (e.g., that each criterion has at least one level, with no two levels equal) and initializing the agent's preferences (a PreorderedSet) with the alternatives and the inferences that can be made between them by assumption (e.g., dominance). Another parameter to vda is find_best, which specifies the goal of VDA. If find_best is an integer n, Artiruno will only try to find the top-n subset, whereas if find_best is not provided, Artiruno will try to construct a total preorder among all the alternatives.
In its main loop, vda searches for two items to compare. The set of candidate item pairs to_try is initialized with all pairs of alternatives. Pairs whose relations are already known (e.g., by dominance, or from questions the user was previously asked) are removed, and when find_best is provided, item pairs in which neither item could be in the top-n subset are also removed. The remaining pairs are considered one by one, in a lexicographic order that selects more-preferred criterion values (according to how the user defined the criteria originally) first. Within this loop, sets of criteria are themselves looped over (in the same order the criteria were defined), choosing a criterion (or set of criteria) to vary for the first item of the pair and another criterion (or set of criteria) to vary for the second item. Artificial items that vary from the best possible items on the chosen criteria are constructed in the fashion of R(σ, p), towards the application of segmentwise dominance, as described above. If the relation between these items is unknown, the agent is asked to judge them. The agent may answer that the first item is better, the second is better, or that the two items are equally preferable (Figure 1). Artiruno then updates its PreorderedSet with the response. Given some patterns of responses, it can apply the rule of segmentwise dominance to make further updates.

The multilevel aspect of Artiruno is realized in how it selects the sets of varying criteria for the questions it asks the agent. Initially, Artiruno varies only two criteria: one for the first item, and one for the second. If all applicable questions have been asked and the goal is still unreached, Artiruno increases the threshold to three, allowing two criteria to vary for one item and one criterion to vary for another. This process continues up to double the number of criteria, or to a limit set by the user.
The return value of vda is the PreorderedSet representing the agent's preferences in its final state. This preorder can be characterized with a graph, or in the case of find_best = 1, a sentence such as "Your choices imply a single best alternative: MicroCo.".
Comparison with other methods
It may be instructive to compare Artiruno to some other VDA methods in detail.
ORCON_Z (Moshkovich & Mechitov, 2018),1 a version of ZAPROS, is implemented as a Microsoft Excel spreadsheet with macros. It limits the number of criteria to 6, and the number of levels to 5 per criterion. It requires the user to express a preference for every pair of criterion levels, rather than skipping questions deducible from previous questions and stopping as soon as the decision-making goal is achievable. The user decides between levels of different criteria in isolation, rather than deciding between complete hypothetical items that differ on the chosen criterion levels as in Artiruno. When the user expresses inconsistent preferences, ORCON_Z points out the inconsistency and allows preferences to be corrected. (Artiruno, by not asking questions whose answers it can deduce, gives the user no opportunity to express inconsistent preferences in the first place.) ORCON_Z is not multilevel: only two criteria are allowed to vary at a time in the questions asked of subjects. ORCON_Z lacks automated tests.
Comparison with UniComBOS (Ashikhmin & Furems, 2005) is more difficult, since neither a runnable copy of the program nor its source code are available.2 Ashikhmin and Furems (2005) describe UniComBOS as a web browser-based Java applet paired with a server-side Java program. Like ORCON_Z, UniComBOS has the user decide between isolated sets of criterion levels rather than items, but is multilevel in a very similar way to Artiruno (which is no accident, since Artiruno's multilevel support was inspired by UniComBOS). User replies to multilevel questions are used to make inferences about items using a principle of "U-dominance" that serves as an equivalent to segmentwise dominance for partially defined items. UniComBOS's strategy for selecting questions and stopping the interview is unclear, but it appears that for each level of the multilevel procedure, the set of questions asked is exhaustive rather than strategic. Like ORCON_Z, UniComBOS notifies the user of inconsistencies and allows them to be corrected; in fact, it deliberately asks logically redundant questions as consistency checks. Unlike both ORCON_Z and Artiruno, UniComBOS allows the user to answer "I don't know" to a question. This is understood as an assertion of incomparability, so if a different preference could later be inferred for the relation in question, UniComBOS would consider that inconsistent. Artiruno, by contrast, treats incomparability as incomplete information, and works on the assumption that the user's true preferences are a total preorder. UniComBOS lacks automated tests.
DEX (Bohanec & Rajkovič, 1990; Bohanec, 2023; https://repo.ijs.si/markobohanec/dexilibrary) is an MCDA method that primarily uses totally ordered qualitative criteria, and requires no numerical judgments; Bohanec draws comparison to VDA without describing DEX as a form of VDA. DEXi, the latest implementation, is free software, but is written in Oxygene, a proprietary dialect of Pascal. In DEX, criteria are arranged in a hierarchy not unlike that of the AHP, where the root element of the hierarchy represents the overall judgment to be made, such as the quality of a car. Each non-leaf criterion is determined by its child criteria according to a function mapping each tuple of the child levels to a parent level. The user can define the entire function by hand, or use dominance or numerical weights to infer some parts of the function from others (manually entered dominance violations are called out, but allowed). So, as with ORCON_Z and UniComBOS, DEX requires full definition of the decision procedure before consideration of items, rather than providing an adaptive interview like Artiruno, and the user generally makes judgments on the basis of partially defined items. But DEX includes extensions for probabilistic or fuzzy criteria, and it has plenty of automated tests. It also has R and Python interfaces in development as of 2022.
Testing
Artiruno's automated test suite is divided into two parts: one for PreorderedSet alone and one for VDA.
The PreorderedSet tests check that adding consistent relations makes the necessary inferences by transitivity, while adding inconsistent relations raises an exception. They also check example uses of methods such as extreme, used to get top-n or bottom-n subsets, and get_subset, used to make a new PreorderedSet that contains a subset of the original's items while preserving all relations among them.
The VDA tests check various trivial scenarios (where no questions need to asked of the agent, because the goal is attainable by inferences that follow immediately from assumptions) as well as simple scenarios with manually programmed responses from the agent. They also check that VDA can complete successfully on item spaces that would be too large to hold in memory if fully instantiated. The broadest tests examine whether Artiruno can learn randomly generated preferences, so long as a simulated agent makes decisions in accordance with them. Two classes of randomly generated preferences are tested: lexicographic preferences, in which the criteria have a fixed order such that values on a higher-ranked criterion are always more important than values on all lower-ranked criteria, and additive utility functions, in which each criterion level adds a certain positive amount of utility. The random generation of preferences is seeded, and the total number of questions asked to reach the VDA goal (also randomized) is tracked, so any changes to Artiruno that result in more questions needing to be asked for the same test case can be noticed.
An extended example
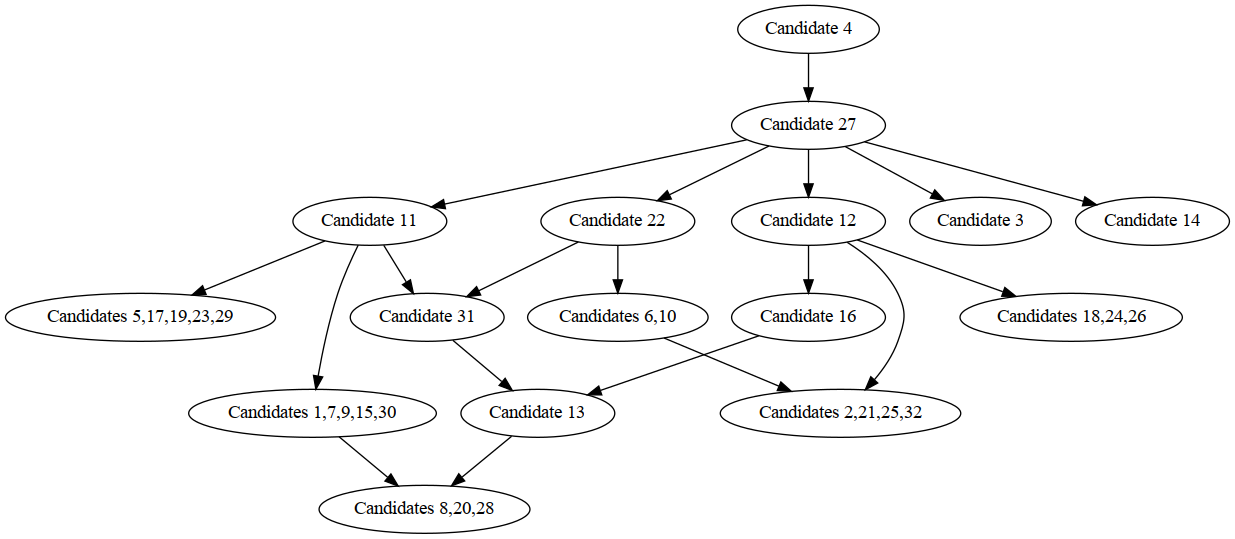
For an example of how Artiruno would operate when used with a larger problem, consider the faculty-selection scenario of Moshkovich and Mechitov (2018). We use four criteria (A, B, C, D) with three levels each, and we set find_best = 2, as if deciding on the two best candidates to consider for the next round of faculty selection. Table 3 of Moshkovich and Mechitov (2018) lists 32 alternatives, but several are equal to each other on all criteria, which is forbidden by Artiruno, since VDA offers no way to distinguish them. Thus, we begin by collapsing identical candidates into single alternatives (e.g., candidates 6 and 10 become the alternative "Candidate 6,10"), leaving 16 alternatives. This problem setup is distributed with Artiruno's source code in the file examples/faculty.json.
Artiruno initializes the set to_try with all (16 choose 2) = 120 pairs of alternatives. This set is immediately reduced to 82 pairs by removing pairs for which the preference relation can be inferred by dominance: for example, candidate 4 (A3, B3, C3, D2) dominates candidate 22 (A3, B3, C2, D2), being non-inferior on all criteria and superior on C. We reduce to_try further to 23 pairs by removing pairs containing an alternative known to be worse (by dominance) than 2 or more other alternatives—such an item must not lie in the top-2 subset.
Now we can select the first element of to_try, which is the pair of items a = (A3, B2, C3, D2) and b = (A3, B3, C2, D2). There are two criteria on which these items differ: B and C. Thus, we check for preferences regarding R({B}, a) vs. R({B}, b), R({C}, a) vs. R({C}, b), R({B}, a) vs. R({C}, b), and R({C}, a) vs. R({B}, b). The first two relations follow from dominance: they are R({B}, a) < R({B}, b) and R({C}, a) > R({C}, b), respectively. The third does not, so we ask the user to decide between them, that is, to say which of (A3, B3, C2, D3) and (A3, B3, C3, D2) is better. Suppose the user chooses the former. Then R({B}, a) > R({C}, b), and since R({C}, a) = (A3, B3, C3, D3) = R({B}, b), we may conclude a > b by segmentwise dominance.
We continue in this way, filtering out pairs from to_try whose relations are known or that contain items deducible to be outside the top-2 subset, taking the first remaining element of to_try, and attempting to use segmentwise dominance to find their relation, asking the user when necessary. The exact process depends on the user's answers to the questions about hypothetical items. If the user chooses the second option to the subsequent three questions, this suffices for Artiruno to conclude that the top-2 subset is {candidate 4, candidate 27}, with candidate 4 being better. Figure 2 shows the inferred preferences among the alternatives. The user is thus recommended to advance these two candidates to the next round of selection.
find_best, at the cost of asking the user more questions.Empirical study
Artiruno's automated tests ensure that it behaves as intended in artificial situations, but leave open the question of how well it works in practice. Seeing as Artiruno is a tool to improve decision-making, one may well ask: does using it result in better decisions? To answer this question, I conducted an experiment in which people considered an important decision they had to make in real life. Some subjects were randomly assigned to use Artiruno to help make this decision, while others received no special guidance. I used a no-treatment control condition, rather than a different formal decision-making method, to better capture the effect of Artiruno in contrast to the usual case in real life, where we make decisions without some formal method or scientist advising us how to do it. This scheme offers no ability to tease apart which of Artiruno's components is responsible for any observed between-condition effects, but avoids confusing the effect of Artiruno per se with the effect of another method. I had subjects use Artiruno by themselves, rather than receiving expert help, to keep the treatment effect from being confounded with the effect of third-party input on the decision-making process.
The task code can be found at https://github.com/Kodiologist/Artiruno-task. The raw data, analysis code, and a research notebook (for this study and for several pilot studies not reported here) can be found at http://arfer.net/projects/artiruno.
Method
Subjects were recruited from Prolific, an England-based web service that allows users to enroll in paid online human-subjects research. The study was implemented as a web application split into three phases: screening, the main or "scenario" phase, and a follow-up. Internally (i.e., in terms of the task code and its database), each phase corresponded to one session except that the scenario phase was split into two sessions, one before condition assignment and one after, to keep subjects from changing their earlier answers after being assigned a condition. In terms of Prolific, each phase was represented as a separate study.
Screening
The screening phase was open to all Prolific users whose first language was English, according to a questionnaire that users filled out as part of registration to use Prolific. This phase took place in February and March of 2023 and paid subjects $1 US, or the equivalent in another currency. After completing a consent form, subjects were told "This study will ask you to describe an important decision that you've thinking about but you haven't made yet. Ideally, it's a decision that you'll have made and seen some consequences of (good or bad) within the next month." They were given 11 examples of decisions they might consider (see appendix for full instructions for all phases), asked "Do you have a decision of this kind to make?", and told "If yes, briefly describe it."
Aiming to have at least 20 subjects in each condition complete all phases, and expecting a follow-up rate of about half, I screened subjects until at least 40 in each condition had completed the scenario phase.
Scenario phase
Among those who answered "yes" to the yes-or-no question in screening, I informally judged whether the described decision situation was an appropriate fit for Artiruno. If so, I invited the subject to continue to the next phase, which paid $4.
The phase began with a simple logic puzzle, which prevented the subject from continuing with the study until they provided the correct answer. The purpose of this obstacle was to reduce dropout after conditions were assigned by encouraging dropout earlier. Next, subjects described a decision situation that they wanted to consider for this study. The instructions and examples were substantially the same as in the screener; subjects were told they could use the same scenario they mentioned in the screener or a new one. They were also asked "Approximately, what is the latest date by which you think you'll have made the decision, and you'll be able to say whether you're happy with the choice you made?"
At this point, subjects were randomly assigned to the control condition or the VDA condition. (Conditions were assigned by building a sequence of randomly permuted two-condition subsequences and then assigning each subject the last unused condition. This scheme ensured a random uniform distribution of conditions across subjects, while maximizing the equality of sample sizes among conditions.) Control subjects skipped to the demographics questionnaire (described below). VDA subjects encoded their situation into criteria and alternatives of the kind expected by Artiruno. They were given written instructions, two examples, and a web-form interface (Figure 3). The task program only allowed subjects to continue if their responses passed some non-triviality checks. There had to be at least two alternatives, at least two criteria, and at least two levels of each criterion. Names had to be sufficiently distinct (e.g., no two alternatives could have the same name), and no two alternatives could be equal on all criteria. Failed checks were explained with a dialog box. A final check, for any alternatives that dominated all others, produced a detailed warning ("This situation usually arises by mistake. For example, you may've forgotten to include a criterion that makes the other alternatives more appealing than [dominator] in some way.") but allowed subjects to continue if they felt that dominance characterized their situation correctly.

With criteria and alternatives in hand, VDA subjects could begin Artiruno's VDA procedure, using Artiruno version 0.4.1
and find_best = 1 (meaning that Artiruno would try to find the single best alternative). Buttons allowed subjects to restart VDA or return to editing criteria and alternatives in case they made a mistake. The VDA procedure per se was skipped for subjects who had defined a dominator, since Artiruno's recommendation was already determined. Instructions emphasized that the recommendation produced by the software was only a recommendation, and subjects were free to make their own decision.
Finally, all subjects completed a short demographic questionnaire, which asked for their country of residence, age, gender, race or ethnicity, and years of education completed.
Follow-up
At least 4 weeks after completing the scenario phase, subjects were sent a message through Prolific: "In the previous session, you said you expected to face this decision: '…'. I'd like to invite you to another session once you've made this decision and gotten to see at least a little of the outcome. Have you yet? If not, suggest a date (in the format YYYY-MM-DD) on which you'd like me to ask you again." Once subjects said they were ready, they were invited to complete the next phase, which paid $4.
In the follow-up phase, subjects were asked to briefly describe in prose "what choice you made", "the outcome", and "how satisfied you are". They then rated three items on 5-point scales: "how satisfied you are with this outcome" (5 = "Very satisfied", 1 = "Not at all satisfied"), "Given only what you knew at the time you made your choice, how good do you think your decision was?" (5 = "A very good decision", 1 = "A very bad decision"), and "How difficult did it feel to make the decision?" (5 = "Very easy", 1 = "Very hard"). VDA subjects were then reminded of their criteria and alternatives and Artiruno's conclusion and rated three more items: "How similar do you feel your choice was to this recommendation?" (5 = "Very similar", 1 = "Not at all similar"), "How difficult did it feel to choose the criteria and alternatives, and to answer the hypothetical questions (if any) asked by the program?" (5 = "Very easy", 1 = "Very hard"), and "How helpful did the whole procedure feel for making your decision? (By 'the whole procedure', I mean choosing the criteria and alternatives, answering any hypothetical questions, and getting a recommendation from the program.)" (5 = "Very helpful", 1 = "Not at all helpful").
Results
Subjects
The flow of subjects through the various stages of the study was as follows:
- 130 subjects consented to the study and completed the screening phase.
- 118 subjects were invited to the scenario phase.
- 107 subjects completed the puzzle in the scenario phase.
- Of these, 54 subjects were assigned to the control condition and 53 to the VDA condition.
- 53 control subjects and 42 VDA subjects completed the scenario phase.
- 32 control subjects and 30 VDA subjects completed the follow-up phase.
Notice the differential mortality during the scenario phase, despite the puzzle: only 1 control subject failed to finish the phase after being assigned to their condition, compared to 11 VDA subjects. Presumably the VDA dropout was due to the greater effort required to complete the condition. A small amount of differential mortality in the opposite direction may have occurred later, with 40% of eligible control subjects being lost to follow-up, compared to 29% of VDA subjects.
Of the 95 subjects who completed the scenario phase, and thus the demographic questions, 39% were female and none were nonbinary. Ages ranged from 19 to 68 with a median of 33. Years of education ranged from 8 to 25 with a median of 16. Most subjects (67%) lived in the United Kingdom; 28% in the United States; 3% in continental Europe; and the sole remaining subject in South Africa. In terms of race and ethnicity, 86% of subjects were white; 5% were Asian; 4% were black; 2% were Hispanic; two subjects provided a write-in race of "mixed"; one wrote in "European"; and none were Pacific islander, native American, or Middle Eastern or North African. Note that subjects could endorse more than one race or ethnicity item, in addition to the optional write-in space.
Scenario phase
The subjects who completed the logic puzzle took a median time of 3 min 12 s, and 69% of them gave the correct answer on their first attempt.
| Control | VDA | Topic of decision situation |
|---|---|---|
| 18 | 16 | Employment and business |
| 11 | 7 | Changing homes and emigration |
| 6 | 5 | Health and medical procedures |
| 6 | 3 | Purchases and finance |
| 3 | 4 | Dating and marriage |
| 2 | 4 | Voting |
| 3 | 1 | Vacationing and travel |
| 3 | 0 | Having children |
| 1 | 2 | Education |
Subjects considered a wide variety of decision scenarios, from the question of which of several job offers to take, to the question of whether to have a child (Table 1). Among the 42 subjects who completed VDA with Artiruno, the number of questions Artiruno asked was in general reasonably low: 13 subjects were asked no questions (because they defined a dominating alternative), 12 were asked only one, 4 were asked two, 7 were asked three, 1 was asked four, and the remaining 5 were asked seven, eight, or nine questions. Thus Artiruno usually needed little additional input from the user, after defining criteria and alternatives, to come up with an answer. Artiruno succeeded in finding a single best alternative for all but one subject, for whom Artiruno recommended all alternatives as equivalent.
Among these same 42 VDA subjects, I counted how many provided criteria and alternative definitions that were potentially problematic for Artiruno, or who were subject to unhelpful behavior from Artiruno:
- 19 subjects specified an alternative that dominated another of their alternatives.
- 13 specified an alternative that dominated the full set of alternatives.
- 18 defined a criterion level not used by any alternatives. (Artiruno may still have asked these subjects about hypothetical items with the unused level, if it was the best level for its criterion.)
- 12 defined a criterion for which all alternatives had the same level.
- 6 were asked a question by Artiruno in which all criteria varied.
- 8 were asked by Artiruno to decide between two "hypothetical" items that were actually equal to real alternatives.
None of these anomalies unambiguously indicate user error. Some represent a likely gap between subjects' understanding of the task and how Artiruno works, such as the specification of unused criterion levels. Such situations are readily understandable, because I never explained to subjects how Artiruno works, nor limited the study to people with the technical skills to understand such an explanation. Other anomalies represent inherent limitations in the kinds of situations Artiruno, or VDA more generally, can help with. For example, consider a user who defines two alternatives with two criteria, each with two levels. If one of the alternatives dominates the other, then the best option is already determined. If not, Artiruno can only ask the subject to decide between the alternatives: the problem is too small to be broken down into simpler hypothetical decisions. Ultimately I opted not to exclude subjects from analysis on the basis of these anomalies. To some degree, they represent limitations of Artiruno, for which it is appropriate to penalize the method in an assessment of it.
On the other hand, I do wish to exclude from analysis subjects who appeared to defy the task instructions or otherwise provide nonsensical responses. I rated each subject's VDA setup, including the free-text description, the criteria, and the alternatives, for whether they apparently had either of two problems: a reversed criterion, in which the levels were specified best-to-worst rather than worst-to-best, or a mistakenly set criterion value for an alternative. Since these judgments were subjective, I had a colleague (holding a PhD in decision sciences) independently make the same ratings. Our initial ratings agreed for 81 cases (out of 84, since there were 42 subjects to rate for each of 2 problems). For the remaining 3 cases, we made a final decision after discussion. In the end we rated 6 subjects as defining a reversed criterion and 3 as setting a criterion value for an alternative mistakenly. No subjects had both problems. I decided to exclude 2 additional subjects for idiosyncratic issues: one who defined two alternatives that represented the same choice with different outcomes, and one who defined criteria with no meaningful application to some of the alternatives. I archived my decision to exclude these 11 subjects on 21 Mar 2023 (https://web.archive.org/web/20230321/https://arfer.net/projects/artiruno/notebook#sec--bad-vda-subjects), before running any follow-up sessions, and hence before seeing outcomes.
Follow-up
Of the 32 control subjects and 30 VDA subjects who completed the follow-up phase, the time elapsed between the completion of the scenario phase and the completion of follow-up ranged from 35 to 310 days, with a median of 38.5 days. I include all such control subjects in analysis, while excluding 7 VDA subjects for falling into the aforementioned excluded set. (A sensitivity analysis, in which all the figures and confidence intervals in this section are regenerated with all VDA subjects included, yields substantially similar results.)
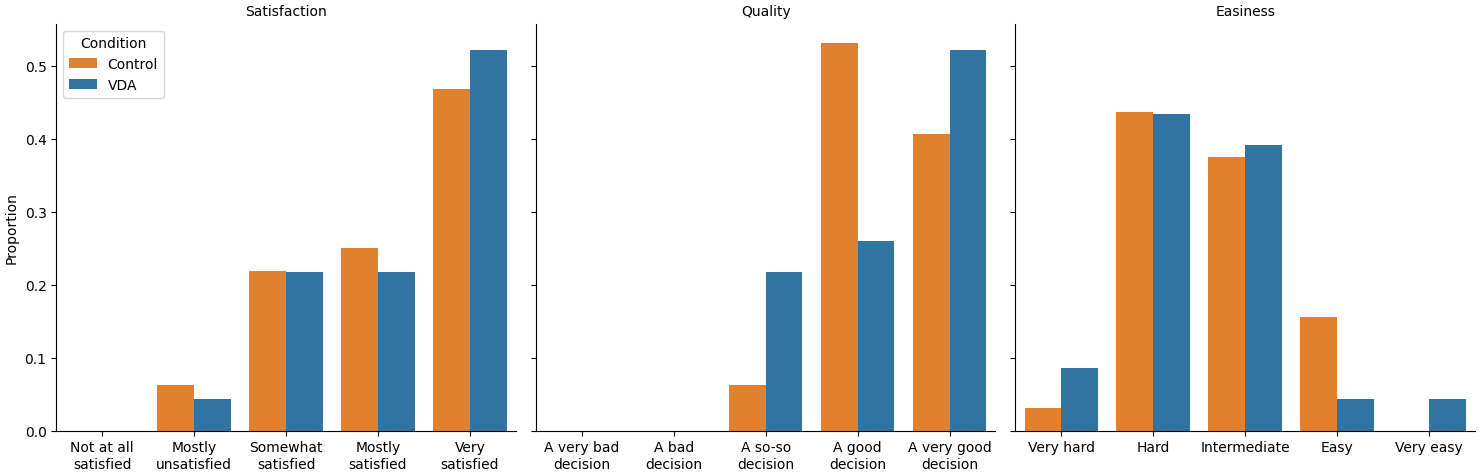
Figure 4 compares the control and VDA subjects on the three common rating items. Overall, subjects were satisfied with their decision outcomes and felt they made a good choice, although they found making the choice to be somewhat difficult. There is at most weak evidence of between-condition differences in mean rating: 95% confidence intervals for the VDA mean minus the control mean are [-0.43, 0.58] for satisfaction, [-0.45, 0.32] for quality, and [-0.53, 0.33] for easiness. I conclude that while Artiruno may increase satisfaction or decrease easiness by as much as .6 scale points, whatever difference exists in quality is quite small, not exceeding about half a scale point. (I compute these intervals with the bias-corrected accelerated bootstrap of Efron, 1987. I use confidence intervals in preference to significance tests due to issues with significance testing pointed out by Cohen, 1994; Wagenmakers, Wetzels, Borsboom, & van der Maas, 2011; and Cumming, 2014; among others.)
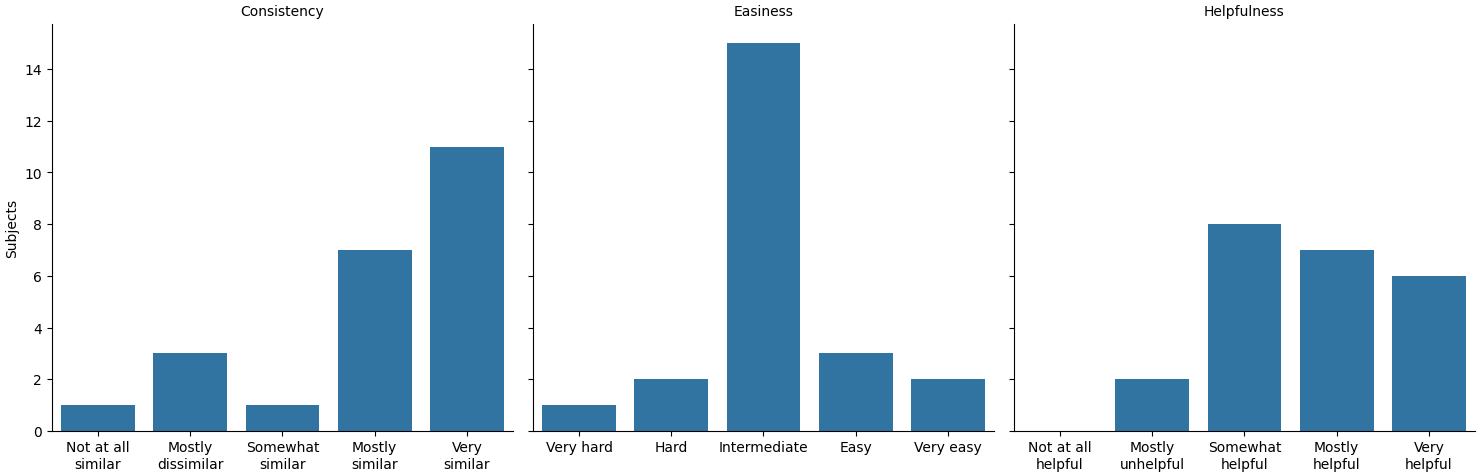
Figure 5 shows how the VDA subjects responded to the Artiruno-specific rating items. Subjects generally judged their choices to be consistent with Artiruno's recommendation, and found Artiruno more helpful than unhelpful, but rated its difficulty of use as intermediate—not hard, but also not easy. A few subjects mentioned in freeform comments that they found Artiruno useful or good; one remarked "although I did not follow the suggestion offered to me, I did find the process of doing this really helpful. It allowed me to give good consideration to the outcomes and possibilities in front of me at the time."
Discussion
Overall, Artiruno may be regarded as a project of mixed success. The empirical study suggests that in a population of non-experts, using Artiruno has little effect on the quality of the decisions that are made or even how people feel about the outcome. But the study also shows that many people with few technical skills can use Artiruno in a competent way for a wide variety of real-life situations given only written instructions, and that Artiruno is unlikely to substantially worsen decisions. Furthermore, automated tests shows that Artiruno satisfies theoretical goals (such as the inference of arbitrary additive utility functions) while advancing VDA methods in the desired fashion (as by tactical selection of questions asked of the agent to reach an agent-specified goal).
There are many ways Artiruno could be extended, which would be facilitated by its public availability as free software. For example, Artiruno departs from the ZAPROS family by eschewing consistency checks, which would add to the number of questions asked of the agent but perhaps result in more accurate representation of preferences. Nor does Artiruno provide an explanation of how the agent's input led to its inferences, possibly creating skepticism about its recommendations. Further improvements could include support for group decision-making, in which the preferences of multiple agents must be harmonized, or support for alternatives that have a missing value for a criterion, or even a fuzzy set of values for a criterion. Finally, Artiruno allows the agent to be indifferent between two options but not to say "I don't know", possibly forcing the agent to make inaccurate or arbitrary judgments.
In the empirical study, we see that while most subjects made suitable use of Artiruno, many others struggled. Difficulty is evident in the drop-out in the VDA condition, in mistakes such as reversing the order of criterion levels, and in subjects' ratings in the follow-up. These findings underscore the value of expert help when it comes to formal decision aid, even for relatively approachable methods like VDA. An MCDA researcher or practitioner would for example easily be able to correct reversed criteria. At the same time, we should appreciate that most subjects could, with no real training, apply an MCDA method (with moderately complex theoretical underpinnings) in a meaningful way to important personal decisions (with largely difficult-to-quantify criteria).
The findings for between-subjects effects on the rating items are disappointing, suggesting that Artiruno failed to meaningfully improve decisions, even though subjects generally made decisions consistent with its recommendation. Perhaps this is because Artiruno usually recommends the same alternative people would choose without its involvement. Or there may be a ceiling effect whereby control subjects were mostly happy with their decisions, leaving little room for improvement; or psychological effects such as dissonance reduction could even have led subjects to feel satisfied regardless of their choice (Brehm, 1956). Ultimately, it may be tempting to infer that Artiruno is inferior to other MCDA methods given these findings, but bear in mind that similar tests are rare. It could be enlightening to see if other MCDA methods can fare better than Artiruno in this kind of situation, a randomized controlled experiment where a general population uses the method by themselves for a personal decision and judges their own satisfaction with the outcome. Conversely, Artiruno's performance in more typical applications of MCDA, where the decision problem is circumscribed to a particular domain in advance, and experts in the method advise the agents, is likewise a question for future research.
References
Ashikhmin, I., & Furems, E. (2005). UniComBOS—Intelligent decision support system for multi-criteria comparison and choice. Journal of Multi-Criteria Decision Analysis, 13(2-3), 147–157. doi:10.1002/mcda.380
Barbosa, P. A. M., Pinheiro, P. R., Silveira, F. R. V., & Filho, M. S. (2019). Selection and prioritization of software requirements applying verbal decision analysis. Complexity. doi:10.1155/2019/2306213
Bohanec, M. (2023). Method DEX. Retrieved from https://dex.ijs.si/documentation/DEX_Method/DEX_Method.html
Bohanec, M., & Rajkovič, V. (1990). DEX: An expert system shell for decision support. Sistemica, 1(1), 145–157. Retrieved from http://web.archive.org/web/20231202134448/https://www.researchgate.net/profile/Marko-Bohanec-2/publication/284679050/links/565840cf08ae4988a7b72b12/DEX.pdf
Brehm, J. W. (1956). Postdecision changes in the desirability of alternatives. Journal of Abnormal and Social Psychology, 52, 384–389. doi:10.1037/h0041006
Cohen, J. (1994). The earth is round (p < .05). American Psychologist, 49(12), 997–1003. doi:10.1037/0003-066X.49.12.997
Cumming, G. (2014). The new statistics: Why and how. Psychological Science, 25(1), 7–29. doi:10.1177/0956797613504966
Edwards, W. (1977). How to use multiattribute utility measurement for social decisionmaking. IEEE Transactions on Systems, Man, and Cybernetics, 7(5), 326–340. doi:10.1109/TSMC.1977.4309720
Efron, B. (1987). Better bootstrap confidence intervals. Journal of the American Statistical Association, 82(397), 171–185. doi:10.2307/2289144
Free Software Foundation. (2008). What is free software and why is it so important for society? Retrieved from http://web.archive.org/web/20080413/https://www.fsf.org/about/what-is-free-software
Gansner, E. R., & North, S. C. (2000). An open graph visualization system and its applications to software engineering. Software, 30(11), 1203–1233. doi:10.1002/1097-024X(200009)30:11<1203::AID-SPE338>3.0.CO;2-N
Hunt, J. M. (2014). Python in CS1: Why change now? Journal of Computing Sciences in Colleges, 30(2). doi:10.5555/2667432.2667468
Ingerman, P. Z. (1962). Algorithm 141: Path matrix. Communications of the ACM, 5(11), 556. doi:10.1145/368996.369016
Kizielewicz, B., Shekhovtsov, A., & Sałabun, W. (2023). pymcdm—The universal library for solving multi-criteria decision-making problems. SoftwareX, 22. doi:10.1016/j.softx.2023.101368
Larichev, O. I. (2001). Ranking multicriteria alternatives: The method ZAPROS III. European Journal of Operational Research, 131(3), 550–558. doi:10.1016/S0377-2217(00)00096-5
Larichev, O. I., & Moshkovich, H. M. (1995). ZAPROS-LM — A method and system for ordering multiattribute alternatives. European Journal of Operational Research, 82(3), 503–521. doi:10.1016/0377-2217(93)E0143-L
Larichev, O. I., & Moshkovich, H. M. (1997). Verbal decision analysis for unstructured problems. Dordrecht, Netherlands: Springer. ISBN 978-1-4419-4777-2. doi:10.1007/978-1-4757-2638-1
Larichev, O. I., Polyakov, O. A., & Nikiforov, A. D. (1987). Multicriterion linear programming problems: Analytical survey). Journal of Economic Psychology, 8(4), 389–407. doi:10.1016/0167-4870(87)90032-8
Mareschal, B. (2013). Visual PROMETHEE 1.4 manual. Author. Retrieved from http://web.archive.org/web/20211108/http://en.promethee-gaia.net/assets/vpmanual.pdf
Millman, K. J., & Aivazis, M. (2011). Python for scientists and engineers. Computing in Science and Engineering, 13(2), 9–12. doi:10.1109/MCSE.2011.36
Moshkovich, H. M., & Mechitov, A. I. (2018). Selection of a faculty member in academia: A case for verbal decision analysis. International Journal of Business and Systems Research, 12(3), 343–363. doi:10.1504/IJBSR.2018.10011350
Moshkovich, H., Mechitov, A., & Olson, D. (2016). Verbal decision analysis. In S. Greco, M. Ehrgott, & J. R. Figueira (Eds.), Multiple criteria decision analysis (2nd ed., pp. 605–636). New York, NY: Springer. ISBN 978-0-387-23081-8. doi:10.1007/978-1-4939-3094-4_15
Saaty, T. L., & Vargas, L. G. (2012). How to make a decision. In Models, methods, concepts & applications of the analytic hierarchy process (pp. 1–21). Boston, MA: Springer. ISBN 978-1489990099. doi:10.1007/978-1-4614-3597-6_1
Sibbald, B., & Roland, M. (1998). Understanding controlled trials: Why are randomised controlled trials important? The BMJ, 316(7126), 201. doi:10.1136/bmj.316.7126.201
Thomas, D. C., & Christensen, B. Y. (2014). Using Python to teach mathematics, physics, and acoustics. Journal of the Acoustical Society of America, 135. doi:10.1121/1.4877003
Wagenmakers, E. J., Wetzels, R., Borsboom, D., & van der Maas, H. L. (2011). Why psychologists must change the way they analyze their data: The case of psi: Comment on Bem (2011). Journal of Personality and Social Psychology, 100(3), 426–432. doi:10.1037/a0022790
Woelfle, M., Olliaro, P., & Todd, M. H. (2011). Open science is a research accelerator. Nature Chemistry, 3(10), 745–748. doi:10.1038/nchem.1149
Notes
See https://verbaldecisionanalysis.wordpress.com. The program itself is archived at: http://web.archive.org/web/20230923143352/https://ulu36w.dm.files.1drv.com/y4mvtR2gUG_xb15CBUh1qb7ix31XAezOBEujOu3vvdoGcIfYe1bEk_3WWJ7bxNZDOt0LpDXYGYAsvwG5s0tjmssqDZxt2auhZV81AvqZYe78g0vgJY8m39R5ItpXrWhnxmXlm3Vr0TJbEHqhBrgUw2OpAC4Rs-fd4GCS2GXzjY3JG6yAe42G1HEVqAHw5QghFRn2F1qUdL8ERDwiKBLYkBUkg
The paper refers to the URL http://iva.isa.ru/DSS, which as of 2023 is dead and not archived in the Internet Archive's Wayback Machine. [Post-publication edit, 6 Jan 2026: you can now find UniComBOS on the Internet Archive at https://archive.org/details/unicombos-0.93]