Pattern notebook
Created 28 Aug 2015 • Last modified 25 Oct 2022
TV 3
The sample size:
(len (ssi sb (= $tv 3)))
| 15 |
How many subjects answered each quiz question correctly:
(.sum (getl quiz (ssi sb (= $tv 3))))
| I | value |
|---|---|
| better-amount | 14 |
| better-prob | 15 |
| immediate | 11 |
| faster-completion | 15 |
The number of subjects who answered every question correctly:
(setv s-tv3-all-correct (list (. (ss (.all (getl quiz (ssi sb (= $tv 3))) 1) $) index))) (len s-tv3-all-correct)
| 10 |
Number of I choices, all TV 3 subjects (recall that there are 60 trials):
(.sort-values (.sum :level "sn" (= (getl ts (ssi sb (= $tv 3)) "choice") "I")))
| sn | choice |
|---|---|
| s037 | 0 |
| s038 | 0 |
| s040 | 0 |
| s041 | 0 |
| s032 | 1 |
| s035 | 2 |
| s033 | 3 |
| s036 | 3 |
| s028 | 5 |
| s026 | 11 |
| s039 | 14 |
| s031 | 20 |
| s030 | 27 |
| s029 | 30 |
| s027 | 35 |
Number of I choices, only TV 3 subjects who answered every quiz question correctly:
(.sort-values (.sum :level "sn" (= (getl ts s-tv3-all-correct "choice") "I")))
| sn | choice |
|---|---|
| s037 | 0 |
| s038 | 0 |
| s040 | 0 |
| s041 | 0 |
| s032 | 1 |
| s036 | 3 |
| s028 | 5 |
| s026 | 11 |
| s031 | 20 |
| s029 | 30 |
Quantiles of the above (expressed as proportions out of 60):
(rd 2 (.quantile (.mean (= (getl ts s-tv3-all-correct "choice") "I") :level "sn") [.25 .5 .75]))
| I | choice |
|---|---|
| 0.25 | 0.00 |
| 0.50 | 0.03 |
| 0.75 | 0.16 |
For comparison, the corresponding quantiles in the 49 subjects of Luhmann, Ishida, and Hajcak (2011) are .17, .43, and .63.
Also for comparison, here's the MTurk subjects:
(.sort-values (.sum :level "sn" (= (getl ts (ssi sb (< $tv 3)) "choice") "I")))
| sn | choice |
|---|---|
| s022 | 0 |
| s017 | 1 |
| s019 | 1 |
| s021 | 1 |
| s023 | 3 |
| s018 | 4 |
| s016 | 6 |
| s003 | 8 |
| s006 | 14 |
| s024 | 27 |
Choices of I after D has become available are still rare. This is the complete list:
(ss (getl ts (ssi sb (<= $tv 3))) (& (> $rt $dwait) (= $choice "I")))
| sn | block | trial | dwait | choice | rt | won | tt |
|---|---|---|---|---|---|---|---|
| s024 | 3 | 1 | 11.568 | I | 13.188 | 4 | 6 |
| s030 | 2 | 1 | 6.392 | I | 11.830 | 0 | 3 |
| s030 | 3 | 3 | 7.716 | I | 9.756 | 0 | 8 |
| s030 | 16 | 3 | 14.593 | I | 14.729 | 0 | 47 |
| s039 | 9 | 2 | 6.995 | I | 8.186 | 4 | 25 |
| s039 | 10 | 3 | 6.849 | I | 9.395 | 0 | 29 |
TV 4
For TV 4, I changed the gamble amounts and probabilities and switched to hypothetical rewards. For TV 5, I reworded the first quiz question.
(.sort-values (.sum :level "sn" (= (getl ts (ssi sb (.isin $tv [4 5])) "choice") "I")))
| sn | choice |
|---|---|
| s049 | 2 |
| s046 | 17 |
| s048 | 18 |
| s047 | 32 |
| s044 | 33 |
| s045 | 33 |
| s042 | 36 |
| s043 | 42 |
(rd 2 (.quantile
(.mean :level "sn"
(= (getl ts (ssi sb (.isin $tv [4 5])) "choice") "I"))
[.25 .5 .75]))
| I | choice |
|---|---|
| 0.25 | 0.30 |
| 0.50 | 0.54 |
| 0.75 | 0.56 |
(learn-scatter (ssi sb (.isin $tv [4 5])))

Here, black dots are I choices and white dots are D choices.
TV 6
Same as TV 5, but with real rewards again.
(.sort-values (.sum :level "sn" (= (getl ts (ssi sb (= $tv 6)) "choice") "I")))
| sn | choice |
|---|---|
| s054 | 1 |
| s057 | 2 |
| s055 | 8 |
| s060 | 22 |
| s050 | 24 |
| s052 | 25 |
| s059 | 27 |
| s053 | 32 |
| s058 | 36 |
| s062 | 36 |
| s051 | 39 |
(rd 2 (.quantile
(.mean :level "sn"
(= (getl ts (ssi sb (= $tv 6)) "choice") "I"))
[.25 .5 .75]))
| I | choice |
|---|---|
| 0.25 | 0.25 |
| 0.50 | 0.42 |
| 0.75 | 0.57 |
Maybe a little less than TV 5, but not bad.
(learn-scatter (ssi sb (= $tv 6)))
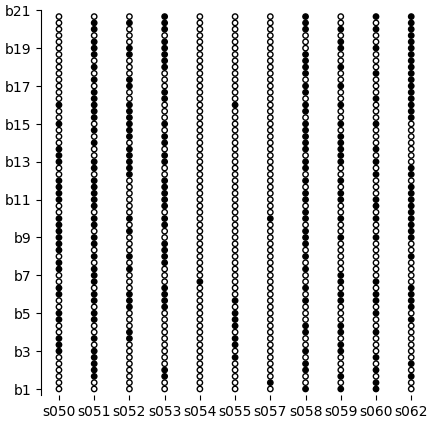
TV 7
Now we're randomly assigning all 4 conditions.
Choices of I after D has already been available for 2 s:
(setv n-late (.sum (.groupby :level "sn" (wc (getl ts s-final) (& (> $rt (+ $dwait 2)) (= $choice "I")))))) (.sort-values :ascending F (get n-late (> n-late 0)))
| sn | value |
|---|---|
| s081 | 22 |
| s160 | 5 |
| s222 | 4 |
| s245 | 3 |
| s244 | 3 |
| s242 | 3 |
| s234 | 2 |
| s080 | 2 |
| s214 | 2 |
| s127 | 2 |
| s104 | 2 |
| s095 | 2 |
| s082 | 2 |
| s164 | 2 |
| s184 | 1 |
| s233 | 1 |
| s230 | 1 |
| s235 | 1 |
| s195 | 1 |
| s068 | 1 |
| s165 | 1 |
| s161 | 1 |
| s152 | 1 |
| s147 | 1 |
| s143 | 1 |
| s142 | 1 |
| s130 | 1 |
| s114 | 1 |
| s107 | 1 |
| s093 | 1 |
| s158 | 1 |
Let's exclude subjects who made 3 or more such errors, or who were inattentive according to the experimenter's notes.
(setv s-late (set (. (get n-late (>= n-late 3)) index)))
(setv s-inattentive #{"s069" "s185"})
(setv s-good (sorted (- (set s-final) s-late s-inattentive)))
(valcounts (getl sb s-good "cond"))
| I | cond |
|---|---|
| control | 42 |
| within_pattern | 43 |
| across_pattern | 42 |
| across_force_d | 42 |
The number of subjects who got each possible number of quiz questions wrong:
(.sort-index (valcounts ($ (getl sb s-final) quiz-qs-wrong)))
| I | quiz-qs-wrong |
|---|---|
| 0 | 94 |
| 1 | 48 |
| 2 | 29 |
| 3 | 3 |
| 4 | 3 |
And here's the number of subjects who got each quiz question wrong:
(.sum (~ (getl quiz s-final)))
| I | value |
|---|---|
| better-amount | 39 |
| better-prob | 15 |
| immediate | 33 |
| faster-completion | 40 |
Subjects per condition getting no quiz questions wrong and satisfying the above criteria:
(valcounts ($ (ss (getl sb s-good) (= $quiz-qs-wrong 0)) cond))
| I | cond |
|---|---|
| control | 23 |
| within_pattern | 21 |
| across_pattern | 23 |
| across_force_d | 22 |
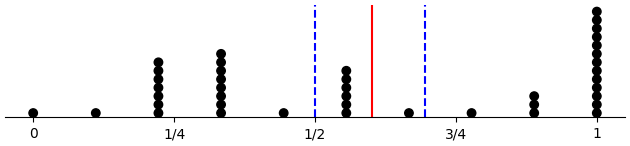
Plots
Here we have the proportion of D choices considering only free-choice trials, which are all 60 trials for control subjects, 30 trials for across-forced subjects, and 20 trials for within-forced subjects. Plots are per condition, with means marked by vertical lines.
(d-prop-dotplot "control")
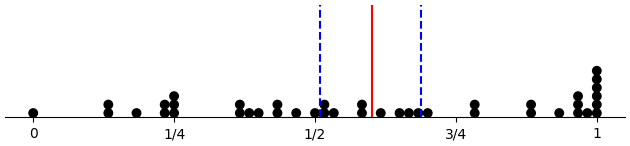
(d-prop-dotplot "within_pattern")
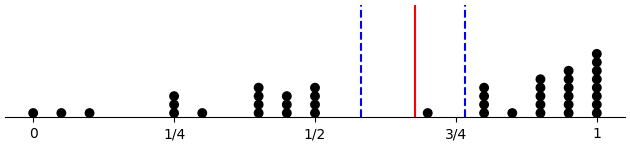
(d-prop-dotplot "across_pattern")
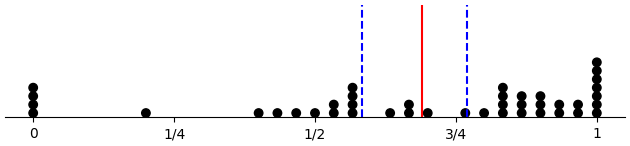
(d-prop-dotplot "across_force_d")
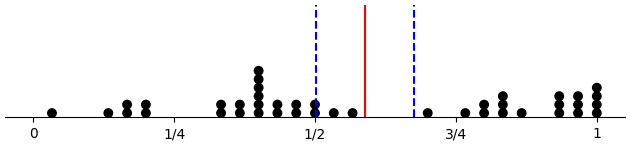
Difference from first to last third
(d-prop-dotplot "control" :diffs T)

(d-prop-dotplot "within_pattern" :diffs T)

(d-prop-dotplot "across_pattern" :diffs T)

(d-prop-dotplot "across_force_d" :diffs T)

Last third only
(d-prop-dotplot "control" :late-only T)
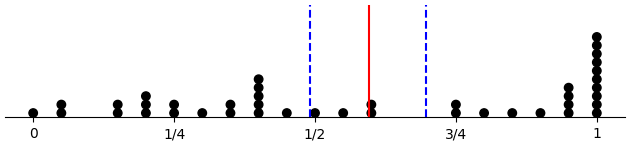
(d-prop-dotplot "within_pattern" :late-only T)
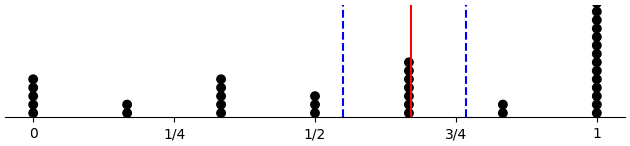
(d-prop-dotplot "across_pattern" :late-only T)
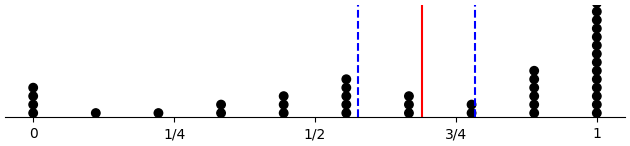
(d-prop-dotplot "across_force_d" :late-only T)
Paper intro notes
- discuss self-control problems and notions of self-control
- introduce teleological behaviorism (Rachlin (2017) - describes teleological behaviorism; Rachlin (2019) - theory: behavioral evolution can select behavior patterns that are beneficial as a pattern but comprise deleterious individual actions )
Hard commitments
Rogers, Milkman, and Volpp (2014) Bryan, Karlan, and Nelson (2010) are review articles about the value of commitment devices
- Read and van Leeuwen (1998) demonstrates hot-to-cold as well as cold-to-hot empathy gaps
- Bryan et al. (2010): rotating savings and credit associations (ROSCAs) can help people to repeatedly choose to save money by committing them to it
- Read, Loewenstein, and Kalyanaraman (1999): when people chose three movies to watch in advance, rather than choosing each movie before watching it, they were more likely to choose highbrow movies. Likewise, they were likelier to choose prize-draw lottery tickets over instant-win tickets when choosing in advance.
- Giné, Karlan, and Zinman (2010): when smokers were given the opportunity to put money in a savings account that they only got back if they stopped smoking, they stopped at a higher rate than controls
- Ariely and Wertenbroch (2002): sort of relevant. Students did better when giving themselves future deadlines. This is like pattern-setting because it's a commitment to future virtuous behavior.
Soft commitments
- Possibly relevant: Bryan et al.'s (2010) definitions: "We refer to commitment devices that call for real economic penalties for failure, or rewards for success, hard commitments. And we refer to any device that has primarily psychological consequences a soft commitment."
- discuss Rachlin's idea of soft commitment for setting the pattern (Rachlin (2016) - describes pattern-setting via "soft commitment" (7 citations, but hasn't been tried) ; Rachlin (2014) is the pop version) - this is a somewhat different definiton of "soft committment" from Bryan et al. (2010); Howie says "Soft commitment is another name for patterning behavior over time so that it may come into contact with temporally distant or extended contingencies."
- Siegel and Rachlin (1995) can be seen as a partial test, but doesn't really test the idea of pattern-setting to improve self-control or increase LL choices - Siegel and Rachlin (1995) found that 4 pigeons who preferred an SS reward over an LL one would instead go for LL if they had to peck keys 31 times instead of 1 time to get an outcome, even though the outcome only depended on the 31st choice. Siegel and Rachlin described this as a (soft) committment although it's clearly different from a case in which the pigeons had to make one choice on whether they were getting SS or LL for a number of remaining trials.
Finally…
- discuss the Newman task (modeled on Luhmann et al. (2011) , which has a planned replication in Ciria et al. (2021) )
Others?
Other possible relevant empirical results to look for or discuss:
- Studies of gym memberships. Do longer memberships increase exercise usage?
- Commitments to diets or swearing off drugs.
- Adherence to diets as affected by buying a lot of food in advance.
Park, Kim, Jhang, Lee, and Lee (2022): a weird paper that's probably not relevant. The gist is that COVID-19 threat pushes people to be more likely to make sequence of choices that make a nice pattern, compared to less patterned sequences.
References
Ariely, D., & Wertenbroch, K. (2002). Procrastination, deadlines, and performance: Self-control by precommitment. Psychological Science, 13(3), 219–224. doi:10.1111/1467-9280.00441
Bryan, G., Karlan, D., & Nelson, S. (2010). Commitment devices. Annual Review of Economics, 2(1), 671–698. doi:10.1146/annurev.economics.102308.124324
Ciria, L. F., Quintero, M. J., López, F. J., Luque, D., Cobos, P. L., & Morís, J. (2021). Intolerance of uncertainty and decisions about delayed, probabilistic rewards: A replication and extension of Luhmann, C. C., Ishida, K., & Hajcak, G. (2011). PLOS ONE. doi:10.1371/journal.pone.0256210
Giné, X., Karlan, D., & Zinman, J. (2010). Put your money where your butt is: A commitment contract for smoking cessation. American Economic Journal: Applied Economics, 2(4), 213–235. doi:10.1257/app.2.4.213
Luhmann, C. C., Ishida, K., & Hajcak, G. (2011). Intolerance of uncertainty and decisions about delayed, probabilistic rewards. Behavior Therapy, 42, 378–386. doi:10.1016/j.beth.2010.09.002. Retrieved from http://www.psychology.stonybrook.edu/cluhmann-/papers/luhmann-2011-bt.pdf
Park, J., Kim, J., Jhang, J., Lee, J. C., & Lee, J. (2022). The impact of infectious disease threat on consumers' pattern-seeking in sequential choices. Psychology and Marketing, 39(2), 370–389. doi:10.1002/mar.21602
Rachlin, H. (2014, July 24). If you're so smart, why aren't you happy? Retrieved from http://blog.oup.com/2014/07/psychology-self-monitor-abstract-particular
Rachlin, H. (2016). Self-control based on soft commitment. Behavior Analyst, 39(2), 259–268. doi:10.1007/s40614-016-0054-9
Rachlin, H. (2017). In defense of teleological behaviorism. Journal of Theoretical and Philosophical Psychology, 37(2), 65. doi:10.1037/teo0000060
Rachlin, H. (2019). Group selection in behavioral evolution. Behavioural Processes, 161, 65–72. doi:10.1016/j.beproc.2017.09.005
Read, D., Loewenstein, G., & Kalyanaraman, S. (1999). Mixing virtue and vice: Combining the immediacy effect and the diversification heuristic. Journal of Behavioral Decision Making, 12(4), 257–273. doi:10.1002/(SICI)1099-0771(199912)12:4<257::AID-BDM327>3.0.CO;2-6
Read, D., & van Leeuwen, B. (1998). Predicting hunger: The effects of appetite and delay on choice. Organizational Behavior and Human Decision Processes, 76, 189–205. doi:10.1006/obhd.1998.2803
Rogers, T., Milkman, K. L., & Volpp, K. G. (2014). Commitment devices: Using initiatives to change behavior. JAMA, 311(20), 2065–2066. doi:10.1001/jama.2014.3485
Siegel, E., & Rachlin, H. (1995). Soft commitment: Self-control achieved by response persistence. Journal of the Experimental Analysis of Behavior, 64(2), 117–128. doi:10.1901/jeab.1995.64-117