Pattern-setting for improving risky decision-making
Created 10 Apr 2022 • Last modified 9 Dec 2022
Self-control can be defined as making choices in accordance with long-term, rather than short-term, patterns of behavior. Rachlin (2016) suggested a novel technique to enhance self-control, by which individual choices carry the weight of a larger pattern of choices. This report describes a study of 169 college students who made repeated choices between two gambles. The better of the two gambles had a greater win probability but required waiting an uncertain amount of time. Some "patterned" subjects were forced to repeat their previous choices according to a schedule, while control subjects could choose freely on every trial. It was found that on free-choice trials, the patterned subjects chose the better gamble more often than controls. There was stronger evidence for such an effect appearing immediately than for it developing gradually from a process of learning over the course of the task. An additional condition in which subjects were forced to choose the better gamble yielded inconsistent results. Overall, the results support the use of pattern-setting as a strategy to improve decision-making.
This paper was published as:
Arfer, K. B. (2023). Pattern-setting for improving risky decision-making. Journal of the Experimental Analysis of Behavior, 119, 81–90. doi:10.1002/jeab.816
The official Wiley PDF has only minor differences from this the original document.
Keywords: self-control, response patterns, behavioral economics, risk taking, humans
Acknowledgments
This study was originally conceived and designed in 2015 in close collaboration with Howard Rachlin. I wrote this manuscript and conducted new analyses for it after his death.
Introduction
Failures of self-control are an all-too-familiar experience in human life, ranging from the mundane problem of eating too much of something tasty and getting a bellyache, to the potentially lethal crisis of severe drug addiction. But defining self-control, that is, defining behavior that constitutes a self-control success or a self-control failure, is fraught with difficulty. Rachlin (2017) proposed that self-control is behavior that is directed by higher-level, more temporally extensive goals, such as being healthy, in contrast to immediate goals, such as the short-term pleasure of another bite of food. This approach naturally fits into what Rachlin calls teleological behaviorism, the view that an organism's mind is best identified with the complex set of overlapping, often very long-term behavioral patterns that direct its behavior over its life (Rachlin, 1992; Rachlin, 2014a; see also Simon, 2023). Individual moment-to-moment actions, such as walking one step, occur as part of larger goal-directed behaviors, such as going to work, and patterns telescope outwards in this fashion until we reach the organism's highest-order, most abstract goals, such as being a good person or living a fulfilling life. To act with self-control, then, is to act in accordance with a long-term and important pattern rather than a competing shorter-term and less important pattern.
If an agent's long- and short-term behavioral patterns are in conflict, and obeying the longer-term patterns is to its benefit, then the agent may benefit from being committed to obeying the longer-term patterns. Thus the value of commitment devices, by which agents can reduce temptation or the opportunity to renege on a goal (Bryan, Karlan, & Nelson, 2010; Green & Rachlin, 1996; Rachlin & Green, 1972; Rogers, Milkman, & Volpp, 2014). For example, Giné, Karlan, and Zinman (2010) found that when smokers were given the opportunity to put money in a savings account that they only got back if they stopped smoking, they quit at a higher rate than controls. Although not forced to stop smoking, the smokers in the savings-account group had been given a monetary incentive to avoid this self-control failure. Bryan et al. (2010) discuss rotating savings and credit associations (ROSCAs), which provide an incentive to save money by requiring regular saving to get one's share of a communal pot. In a ROSCA, a number of savers meet periodically. At each meeting, everybody contributes an equal amount, and one person is awarded all the contributions. The awardee rotates from meeting to meeting, so eventually, every member gets an equal share.
Monetary incentives, however, aren't the only sort of commitment that ROSCAs provide. ROSCAs are small organizations, generally formed among people who already know each other, and that presumably lead to social pressure to continue saving. This softer kind of commitment, compared to losing money, may still be effective. Rachlin (2016) proposed an especially soft commitment strategy called pattern-setting (previously described in Rachlin, 2014b). The idea is that once a person has identified a self-control problem, such as an addiction to cigarettes, they begin by getting into the habit of recording how often they do the undesirable behavior. Then they set up a schedule of "pattern days" and "free days". On pattern days, they're obliged to do the behavior as many times as they did in the foregoing free day; for example, they must smoke the same number of cigarettes, no more and no less. Rachlin argues that by establishing large numbers of pattern days, the person will learn to associate each instance of the undesirable behavior on free days with its longer-term effect on pattern days. Thus, a smoker may opt to smoke less on a free day because one cigarette is no longer just one cigarette; instead, the one cigarette implies three or five or seven cigarettes smoked over the succeeding pattern days. If successful, this strategy would be a direct way to bring one's behavior into alignment with longer patterns, and thereby increase self-control, despite never requiring or even explicitly incentivizing reduction of the undesirable behavior.
Read, Loewenstein, and Kalyanaraman (1999) examined a situation similar to pattern-setting in a study of choice for movies. People were given a list of movies they could watch, some "highbrow" and some "lowbrow", on dates of their choice, one movie per day. They either selected each movie they would watch on the day they would watch it or selected three movies in advance to watch. Read et al. found that those choosing movies in advance were more likely to choose highbrow movies, supporting the idea that choosing in advance leads to more frequent "virtuous" (larger-goal-congruent) choices. Siegel and Rachlin (1995) examined various conditions in which pigeons chose between smaller-sooner (SS) and larger-later (LL) food reinforcers. When only one key peck was required per reinforcer, all subjects preferred SS. When 31 pecks were required, however, the pigeons came to prefer LL, even though only the 31st peck actually determined the reinforcer outcome, meaning that a pigeon who pecked the LL key 30 times in a row could still change back to SS on the 31st trial. Thus, behaving in larger units seems to have nudged the pigeons towards the larger reinforcer that required more patience.
The present study used a risky decision-making task based on Luhmann, Ishida, and Hajcak (2011) (to be replicated by Ciria et al., 2021) in which human subjects could choose between two gambles, one of which had a greater probability of paying out than the other but was only available after a delay. The analogy with the smoking-cessation pattern-setting scenario described earlier is that the better gamble is like not smoking: it may be a less appealing choice in the moment, but choosing it frequently has better long-term outcomes. In the current study, some subjects could choose freely on every trial, some were forced to repeat past choices according to one of two patterns, and some were forced to choose the better gamble on certain trials. It was predicted that over the course of the task, as they experienced the gamble outcomes and won the better gamble more often than the worse one, subjects would increasingly choose the better gamble in free-choice trials. Moreover, this effect was predicted to be stronger among subjects in the pattern conditions. It was predicted not to be stronger among those subjects who simply were forced to take the better gamble, because the theory behind pattern-setting (of individual free choices taking on greater weight) doesn't apply in this case.
Method
Task code, raw data, and data-analysis code can be found at http://arfer.net/projects/pattern.
Subjects
A total of 177 undergraduate students in the psychology department of Stony Brook University completed the experiment in September, October, and November of 2015. The first 110 subjects were paid their winnings from the task in cash, but because of limited funds, the remaining 67 completed the task with hypothetical gambles instead. All subjects received course credit.
Procedure
After providing informed consent, subjects read detailed instructions for the task (see the Appendix). A four-item quiz tested the subject's understanding and reinforced it by providing them with the correct answer immediately after each question. Subjects then were presented with condition-specific instructions and completed the task. At the conclusion of the experiment, subjects were debriefed.
Task
The core task of the study was a computer-based gambling task adapted from Luhmann et al. (2011). On each trial of the task, subjects chose between two gambles, which were displayed graphically as may be seen in Figure 1. The immediate choice "Immediate" (named "A" in the instructions and interface shown to subjects) had a 60% chance of paying the subject 4 cents, whereas the delayed choice "Delayed" (named "B" for subjects) had a 70% chance of paying the subject 4 cents. Since Delayed provides a higher probability of winning the same amount, it dominates Immediate; that is, it is no worse than Immediate in both probability and amount, and it is better in probability. However, Delayed was not available at the start of each trial whereas Immediate was. The wait until Delayed could be chosen was 5 s plus a random, exponentially distributed amount of time with median 5 s (or equivalently, mean ). The use of an exponential distribution ensured that after the initial fixed 5 s, the expected remaining wait time remained constant, so waiting provided no new information about the time remaining to wait.

When the subject chose a gamble, they were immediately told whether they had won ("WIN! 4 cents") or lost ("0 cents"). However, if they chose Immediate, they then had to wait until the next trial. The duration of this wait was the same as the wait for Delayed to become available, minus any time the subject had already spent waiting for Delayed. Thus, choosing Immediate only let the subject end the trial and see whether they'd won sooner; it didn't let them complete the whole task sooner.
Trials were grouped into 3-trial blocks. Even-numbered blocks (counting the first block as block 1) were shown with a yellow background, and odd blocks used a blue background. The significance of the blocks varied according to which of four conditions the subject was randomly assigned to. Conditions were assigned by building a sequence of randomly permuted four-condition subsequences and then assigning each subject the last unused condition. This scheme ensured a random uniform distribution of conditions across subjects, while maximizing the equality of sample sizes among conditions.
- In the Control condition, subjects could choose freely on all trials.
- In the Within-Pattern condition, subjects could choose freely on trial 1 of each block, but then had to choose the same gamble on trials 2 and 3 of that block.
- In the Across-Pattern condition, subjects could choose freely in odd-numbered blocks, but had to make the same sequence of choices in each even-numbered block as they had in the previous block.
- In the Force-Delayed condition, subjects could choose freely in odd-numbered blocks, but could only choose Delayed in even-numbered blocks.
In all conditions, a reminder of the rules for the current trial were shown on screen, above the gambles. Trials on which the subject wasn't forced to choose a given gamble due to condition-specific rules are termed "free" trials henceforth. All subjects completed 20 blocks of 3 trials; thus, Control subjects made a total of 60 free choices, Across-Pattern and Force-Delayed subjects made 30, and Within-Pattern subjects made 20.
It was predicted that in the two pattern conditions, compared to the Control, there would be a greater proportion of free choices for Delayed in later blocks (after sufficient opportunity for learning). Moreover, it was predicted that there would be a greater effect (that is, more free choices of Delayed) in the Across-Pattern condition, because it enforced a larger-scale pattern. Finally, it was predicted that free choices under Force-Delayed would be similar to those under Control, consistent with the hypothesis that it was pattern-setting, not merely being forced to make choices, that increased free choices for Delayed.
Results
Demographics
Demographic information was obtained from screener forms the subjects filled out as part of registering for the department's subject pool (typically at the beginning of the semester, in August or September 2015). Of the 177 subjects, 65% were female. Ages ranged from 17 to 49, with 95% of subjects being 22 or younger. In terms of ancestry, one item allowed the respondent to choose one of "African American/Black", "American Indian or Alaska Native", "Asian", "Caucasian/White", "Multiple Ethnicity", "Native Hawaiian or Other Pacific Islander", or "Other", and another item asked if the respondent was Hispanic. The result was that 45% indicated they were white, 24% Asian, 12% black, 11% "Other", and 7.9% multiethnic, while 16% were Hispanic. All subjects indicated they were native speakers of English. Finally, 10% were left-handed.
Task
| Condition | Control | Within-Pattern | Across-Pattern | Force-Delayed |
|---|---|---|---|---|
| Total | 44 | 45 | 43 | 45 |
| Compensation | ||||
| Paid | 28 | 28 | 27 | 27 |
| Unpaid | 16 | 17 | 16 | 18 |
| Quiz questions | ||||
| answered incorrectly | ||||
| 0 | 24 | 23 | 24 | 23 |
| 1 | 11 | 13 | 14 | 10 |
| 2 | 9 | 7 | 4 | 9 |
| 3 | 0 | 0 | 1 | 2 |
| 4 | 0 | 2 | 0 | 1 |
| Excluded | ||||
| Inattentive | 0 | 0 | 0 | 2 |
| Late | 2 | 2 | 1 | 1 |
| Included | 42 | 43 | 42 | 42 |
Table 1 shows the number of subjects assigned to condition. Two exclusion criteria were applied: 2 subjects were classified as "inattentive" because one seemed to fall asleep and the other frequently checked her phone, and 6 subjects were classified as "late" because, on 3 or more trials, they chose Immediate after Delayed had been available for 2 s or longer. (Subjects who were frequently late in this sense apparently were not paying close attention to the task, since they chose the worse option even when the better option had already been available for long enough for them to readily notice.) All subjects who met either exclusion criterion are omitted from all further analyses. Table 1 also shows quiz performance and compensation status per condition, but recall that condition was randomly assigned only after the subject had completed the quiz and been told if they would be paid. Completion times for the gambling task (not including the instructions and quiz) ranged from 13 to 23 min, with a mean of 16 min 58 s.
To analyze the choice data, a mixed-effects logistic-regression model was used. The unit of analysis in the model is individual trials, considering only free-choice trials. The dependent variable is the subject's choice, coded as true for Delayed and false for Immediate, so positive effects indicate preference in favor of Delayed. The model has a per-subject random intercept and the following fixed effects:
- An intercept;
- The subject's condition, coded as dummy variables with Control as the reference category;
- Interactions of each condition with
progress, which is the trial number (from 0 to 59) divided by 59. I use an interaction ofprogresswith Control rather than a main effect ofprogressfor ease of interpretation; paid, a dummy variable indicating whether the subject was paid in real money;quiz_wrong, the number of quiz questions answered incorrectly, rescaled to mean 0 and SD 1;odd_block, a dummy variable indicating whether the trial was in an odd-numbered block; andtrial, the within-block trial number, coded as 0, 1, or 2.
The condition variables and their interactions with progress are the predictors of interest, whereas the random intercepts and the other fixed effects are nuisance variables. The main effects of condition reflect overall between-condition differences in choices, whereas progress interactions reflect between-condition differences in how choices changed over the course of the task. odd_block and trial are included as nuisance variables because the block structure and block parity were visually indicated to all subjects (even Control subjects, to whom neither had special significance).
For inferences about the model coefficients, confidence intervals (CIs), rather than significance tests, were employed, consistent with growing awareness of problems with the use of significance-testing (e.g., Cohen, 1994; Cumming, 2014, Gelman & Stern, 2006; Kruschke, 2010; Wagenmakers, Wetzels, Borsboom, & van der Maas, 2011). In particular, CIs support nuanced quantitative judgments of the results of a study in place of the all-or-nothing framework of significance-testing. Significance-testing focuses on a null hypothesis of exactly zero effect that is implausible anyway; studies of very large samples, such as those of Meehl (1990) (p. 205), Standing, Sproule, and Khouzam (1991), and Kramer, Guillory, and Hancock (2014), show that population effects close to but not quite equal to zero are to be expected, so the only reason tests fail to reject null hypotheses in practice is that the sample is too small.
| Term | Model 1 | Model 2 |
|---|---|---|
| (intercept) | +0.79 [+0.01, +1.61] | +0.67 [+0.56, +0.78] |
| Within-Pattern | +0.47 [−0.50, +1.46] | +0.52 [+0.27, +0.78] |
| Across-Pattern | +0.17 [−0.79, +1.12] | +0.83 [+0.61, +1.06] |
| Force-Delayed | −0.22 [−1.16, +0.73] | +0.26 [+0.06, +0.46] |
progress × Control |
−0.33 [−0.68, +0.01] | |
progress × Within-Pattern |
+0.29 [−0.34, +0.94] | |
progress × Across-Pattern |
−0.10 [−0.63, +0.42] | |
progress × Force-Delayed |
+0.11 [−0.36, +0.59] | |
paid |
+0.08 [−0.59, +0.76] | |
quiz_wrong |
−0.86 [−1.18, −0.55] | |
odd_block |
−0.02 [−0.20, +0.16] | |
trial |
+0.19 [+0.10, +0.28] |
Table 2 shows coefficients for this model (Model 1). Positive estimates for the main effects of the two pattern conditions indicate that subjects chose Delayed on free-choice trials more often under patterning, and more so for Within-Pattern than Across-Pattern, whose coefficient is small. The interaction terms with progress indicate that over the course of the task, Control subjects decreased their choices of Delayed whereas Within-Pattern subjects increased them. Notably, the paid coefficient is minimal, but the quiz_wrong coefficient is large. These estimates coincide with small overall differences between the paid and unpaid groups (65% Delayed choices for paid vs. 59% for unpaid)
and large differences between quiz-performance groups, particularly among the minority who performed especially badly (21% Delayed choices among the 6 subjects with 3 or 4 incorrect answers, as compared with 54% among the 74 subjects with 1 or 2 incorrect, and 72% among the 89 subjects with 0 incorrect).
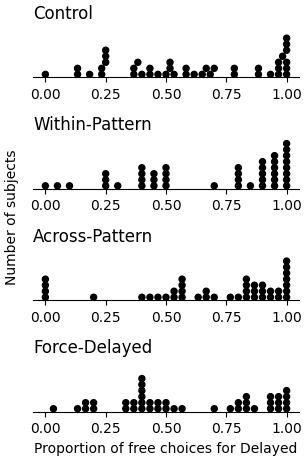
What makes the model difficult to interpret is its wide CIs, meaning that the coefficients are estimated imprecisely. With the idea of trading off accuracy for precision, a much smaller logistic-regression model is also presented. This model has no random effects and uses only dummy variables for the condition (plus an overall intercept) as fixed effects. Furthermore, only the 89 subjects who had answered all the quiz questions correctly are included. This model is less realistic because it fails to account for sources of dependency such as the grouping of choices within subjects and the order in which subjects completed trials, but the smaller set of parameters and the greater homogeneity of subjects makes it easier to estimate. Table 2 (Model 2) shows that the resulting CIs are much narrower, as desired. This model indicates a similar effect as Model 1 for Within-Pattern, but a much larger effect for Across-Pattern and a positive effect for Force-Delayed. In the CIs, the effect of Within-Pattern is at least +0.27 logits and that of Across-Pattern is at least +0.61 logits. Figure 2 shows subjects' choices for Delayed in a simple fashion comparable to Model 2.
Discussion
When people were obliged to repeat choices, they were more likely to choose the better option, that is, the one that required patience. This finding supports Rachlin's (2016) idea of pattern-setting: when their individual choices were given more weight by a pattern structure, the subjects seemed to prioritize a larger goal (earning money, whether real or hypothetical) over a smaller one (ending a momentary period of waiting). There was evidence for the effect of this pattern structure immediately, as well as a tendency for patterning to increase preference for the dominating option, Delayed, over the course of many trials, at least for the Within-Pattern condition.
Across two models, the estimated effects of the conditions can be summarized as follows. The Within-Pattern condition had a consistently positive effect on choices for Delayed, which increased over the course of the task. Across-Pattern had a weakly positive effect in Model 1 that mostly disappeared by the end of the task, contrasted with a strongly positive effect in Model 2. Force-Delayed had a negative effect in Model 1 that was weakened over the course of the task, contrasted with a positive one in Model 2. Control subjects chose Delayed less often over the course of the task. Meanwhile, payment had little relation with the outcome, and subjects who performed badly on the quiz were substantially less likely to choose Delayed.
Overall, the present results suggest that patterning can increase preference for a delayed dominating option. However, it isn't clear whether the shorter immediate pattern (Within-Pattern) is more or less effective than the longer but somewhat delayed pattern (Across-Pattern). Both patterns are still relatively short, leaving open the possibility that stronger effects might be obtainable with longer patterns, such as a single free choice constraining ten future choices. Furthermore, the findings for Force-Delayed are cryptic: perhaps being forced to choose Delayed made subjects want to try the other option more, or perhaps it helped them learn that Delayed was the right choice. The finding that Control subjects chose Delayed less often as the task progressed is contrary to hypothesis and suggests that it is difficult to learn which choice is best without guidance.
The fact that between-condition differences were visible to some extent immediately, as opposed to after a process of learning, is perhaps indicative of the self-knowledge and life experience that subjects brought to the task. People may under-correct for their tendency to make suboptimal decisions, but they are still savvy enough to take opportunities for correction in the first place, as by saving money that they will only be able to get back if they stick to a plan. Recall, for example, that Giné et al. (2010) found that smokers were willing to put money in a savings account that they would only get back if they stopped smoking. Similarly, people participate in ROSCAs although they require regular saving to get any payout. So, once subjects in the pattern conditions understood the special pattern constraints they would be subject to, they may have immediately seen the importance of not committing themselves to the worse gamble in pattern trials. Learning effects might have been strengthened if the pattern constraints had not been explained up front, and subjects had been obliged to learn on their own how the task worked. Such an arrangement would more closely resemble an animal study, but would also entangle what are in principle two distinct learning problems: discovering the task rules and adapting decision-making to those rules.
Considering that condition instructions seemed to suffice to produce the between-condition differences, it may be surprising how poorly subjects performed on the quiz. Only about half correctly answered all four comprehension questions about instructions they had just read. It was intended that the task program's own corrections and the reminder of trial-specific rules shown during each trial would minimize errors, but the especially low preference for Delayed among these poorly performing subjects suggests that they retained misunderstanding about the task. A limitation of the quiz is that it didn't cover condition-specific instructions, and it seems obvious that not all conditions are equally easy to understand. Stronger effects of the conditions, or a greater condition-independent preference for Delayed, might have been observed had subjects understood the task better.
Overall, this laboratory test of the viability of pattern-setting as a self-control technique succeeded, albeit not as fully as expected. Would pattern-setting then be effective for real-world self-control problems, like drug addiction? As with most laboratory studies, it is hard to predict how the effect sizes observed here would translate to substantive decision-making in the field, and whether they would be large enough to be practical. Only a direct empirical test could decide this, but it is worth considering how this study's methods differ from how Rachlin (2016) proposed pattern-setting might be used in the field. First, some subjects were offered hypothetical rather than real money, and studies investigating how hypothetical rewards differ from real ones in risky choice have produced inconsistent results (e.g., Barreda-Tarrazona, Jaramillo-Gutiérrez, Navarro-Martínez, & Sabater-Grande, 2011; Hinvest & Anderson, 2010; Horn & Freund, 2022, Xu et al., 2018; compare with the consistent finding that hypotheticality has little effect on intertemporal choice, as in Johnson & Bickel, 2002; Madden, Begotka, Raiff, & Kastern, 2003; Madden et al., 2004; and Lagorio & Madden, 2005). Second, subjects did not have to monitor and record their own behavior. The task took care of this for them. Not having to do the work of monitoring reduces the barrier to pattern-setting, and hence pattern-setting may be more difficult to use in practice than in this study; on the other hand, Rachlin (2016) suggested that the mere act of monitoring may help change one's own behavior. Third, and perhaps more important, subjects had no choice about obeying the pattern rules. It's one thing to smoke as many cigarettes as you want on Monday and say you'll smoke the same number on Tuesday; it's another to do on Tuesday what you said you'd do, which could itself become a self-control problem. A future test of pattern-setting might try telling subjects what the pattern rule implies they should do, rather than forcing them. Voluntary and consistent compliance with the pattern rule seems necessary for the potential of pattern-setting to be realized.
Appendix
The initial instructions and the quiz were as follows:
Some quick notes before we begin:
- Please give the experiment your undivided attention. Doing something else (like checking your phone) during a waiting period would interfere with the purpose of the experiment.
- This experiment uses timers to make you wait for certain things. Don't use your browser's back button or refresh button on a page with a timer, or the timer may restart (in which case it will have the same length as before).
In this study, you'll complete a number of trials which will allow you to choose between two gambles, A or B. You can win real money from the gambles, which will be paid to you at the end of the study. You can't lose money from gambles. Right after you choose each gamble, I'll tell you whether or not you won the gamble.
[For unpaid subjects, the above instead read "In this study, you'll complete a number of trials which will allow you to choose between two gambles, A or B. You can win (imaginary) money from the gambles. You can't lose money from gambles. Right after you choose each gamble, I'll tell you whether or not you won the gamble. At the end of the study, I'll tell you your total winnings. Although no real money will be involved in this study, please try to make your decisions as if the gambles were for real money."]
Here's what the gambles look like:
[An example similar to Figure 1 of the main manuscript.]
The colored bars are just graphical representations of the chance of winning.
Notice that B has a higher chance of paying out. However, B isn't immediately available at the beginning of each trial. It will show as "[Not available yet]". You'll have to wait a random, unpredictable amount of time (sometimes short, sometimes long) for B to become available.
Choosing A will allow you to receive an outcome (either winning or not winning) without waiting, because A is available from the start of each trial. But choosing A won't let you complete the study any faster, because the time you would have waited for B, had you waited for it, will be added to the time you have to wait to get to the next trial (or to the end of the study). Any time you spend waiting before choosing A (although you don't need to wait before choosing A, as you do for B) will be credited towards reducing this wait.
Let's test your understanding.
- Compared to B, A's chance of paying out is
- lower [correct]
- higher
- the same
- Which gamble gives you more money when you win the gamble?
- A
- B
- They give the same amount of money [correct]
- Which option can you choose as soon as a trial starts?
- A [correct]
- B
- Either A or B
- Which option will allow you to complete the study faster?
- A
- B
- Neither; it makes no difference [correct]
Okay, one more thing before we begin.
You'll complete trials in blocks of 3.
[On a blue background:] In odd-numbered blocks (the 1st, 3rd, 5th, and so on), you'll see this background.
[On a yellow background:] In even-numbered blocks (the 2nd, 4th, 6th, and so on), you'll see this background.
The final line of the instructions varied by condition:
- Control: "The task works the same whether you're in an odd block or an even block."
- Within-Pattern: "Within each block, whether even or odd, you can choose either A or B on trial 1, but the task will force you to repeat that choice on trial 2 and trial 3."
- Across-Pattern: "In odd blocks, you can choose either A or B. In even blocks, the task will force you to repeat the series of choices you made in the previous block. So if in the 1st block you chose A, then B, then A, the task will force you in the 2nd block to choose A, then B, then A."
- Force-D: "In odd blocks, you can choose either A or B. In even blocks, the task will force you choose [sic] B on every trial."
References
Barreda-Tarrazona, I., Jaramillo-Gutiérrez, A., Navarro-Martínez, D., & Sabater-Grande, G. (2011). Risk attitude elicitation using a multi-lottery choice task: Real vs. hypothetical incentives. Spanish Journal of Finance and Accounting, 40(152), 613–628. doi:10.1080/02102412.2011.10779713
Bryan, G., Karlan, D., & Nelson, S. (2010). Commitment devices. Annual Review of Economics, 2(1), 671–698. doi:10.1146/annurev.economics.102308.124324
Ciria, L. F., Quintero, M. J., López, F. J., Luque, D., Cobos, P. L., & Morís, J. (2021). Intolerance of uncertainty and decisions about delayed, probabilistic rewards: A replication and extension of Luhmann, C. C., Ishida, K., & Hajcak, G. (2011). PLOS ONE. doi:10.1371/journal.pone.0256210
Cohen, J. (1994). The earth is round (p < .05). American Psychologist, 49(12), 997–1003. doi:10.1037/0003-066X.49.12.997
Cumming, G. (2014). The new statistics: Why and how. Psychological Science, 25(1), 7–29. doi:10.1177/0956797613504966
Gelman, A., & Stern, H. (2006). The difference between "significant" and "not significant" is not itself statistically significant. The American Statistician, 60(4), 328–331. doi:10.1198/000313006X152649
Giné, X., Karlan, D., & Zinman, J. (2010). Put your money where your butt is: A commitment contract for smoking cessation. American Economic Journal: Applied Economics, 2(4), 213–235. doi:10.1257/app.2.4.213
Green, L., & Rachlin, H. (1996). Commitment using punishment. Journal of the Experimental Analysis of Behavior, 65(3), 593–601. doi:10.1901/jeab.1996.65-593
Hinvest, N. S., & Anderson, I. M. (2010). The effects of real versus hypothetical reward on delay and probability discounting. Quarterly Journal of Experimental Psychology, 63(6), 1072–1084. doi:10.1080/17470210903276350
Horn, S., & Freund, A. M. (2022). Adult age differences in monetary decisions with real and hypothetical reward. Journal of Behavioral Decision Making, 35(2). doi:10.1002/bdm.2253
Johnson, M. W., & Bickel, W. K. (2002). Within-subject comparison of real and hypothetical money rewards in delay discounting. Journal of the Experimental Analysis of Behavior, 77(2), 129–146. doi:10.1901/jeab.2002.77-129
Kramer, A. D., Guillory, J. E., & Hancock, J. T. (2014). Experimental evidence of massive-scale emotional contagion through social networks. Proceedings of the National Academy of Sciences, 111(24), 8788–8790. doi:10.1073/pnas.1320040111
Kruschke, J. K. (2010). What to believe: Bayesian methods for data analysis. Trends in Cognitive Sciences, 14(7), 293–300. doi:10.1016/j.tics.2010.05.001
Lagorio, C. H., & Madden, G. J. (2005). Delay discounting of real and hypothetical rewards III: Steady-state assessments, forced-choice trials, and all real rewards. Behavioural Processes, 69(2), 173–187. doi:10.1016/j.beproc.2005.02.003
Luhmann, C. C., Ishida, K., & Hajcak, G. (2011). Intolerance of uncertainty and decisions about delayed, probabilistic rewards. Behavior Therapy, 42, 378–386. doi:10.1016/j.beth.2010.09.002. Retrieved from http://www.psychology.stonybrook.edu/cluhmann-/papers/luhmann-2011-bt.pdf
Madden, G. J., Begotka, A. M., Raiff, B. R., & Kastern, L. L. (2003). Delay discounting of real and hypothetical rewards. Experimental and Clinical Psychopharmacology, 11(2), 139–145. doi:10.1037/1064-1297.11.2.139
Madden, G. J., Raiff, B. R., Lagorio, C. H., Begotka, A. M., Mueller, A. M., Hehli, D. J., & Wegener, A. A. (2004). Delay discounting of potentially real and hypothetical rewards II: Between- and within-subject comparisons. Experimental and Clinical Psychopharmacology, 12(4), 251–261. doi:10.1037/1064-1297.12.4.251
Meehl, P. E. (1990). Why summaries of research on psychological theories are often uninterpretable. Psychological Reports, 66(1), 195–244. doi:10.2466/pr0.1990.66.1.195
Rachlin, H. (1992). Teleological behaviorism. American Psychologist, 47, 1371–1382. doi:10.1037/0003-066X.47.11.1371
Rachlin, H. (2014a). The escape of the mind. Oxford, England: Oxford University Press. ISBN 978-0199322350.
Rachlin, H. (2014b, July 24). If you're so smart, why aren't you happy? Retrieved from http://blog.oup.com/2014/07/psychology-self-monitor-abstract-particular
Rachlin, H. (2016). Self-control based on soft commitment. Behavior Analyst, 39(2), 259–268. doi:10.1007/s40614-016-0054-9
Rachlin, H. (2017). In defense of teleological behaviorism. Journal of Theoretical and Philosophical Psychology, 37(2), 65. doi:10.1037/teo0000060
Rachlin, H., & Green, L. (1972). Commitment, choice and self-control. Journal of the Experimental Analysis of Behavior, 17(1), 15–22. doi:10.1901/jeab.1972.17-15
Read, D., Loewenstein, G., & Kalyanaraman, S. (1999). Mixing virtue and vice: Combining the immediacy effect and the diversification heuristic. Journal of Behavioral Decision Making, 12(4), 257–273. doi:10.1002/(SICI)1099-0771(199912)12:4<257::AID-BDM327>3.0.CO;2-6
Rogers, T., Milkman, K. L., & Volpp, K. G. (2014). Commitment devices: Using initiatives to change behavior. JAMA, 311(20), 2065–2066. doi:10.1001/jama.2014.3485
Siegel, E., & Rachlin, H. (1995). Soft commitment: Self-control achieved by response persistence. Journal of the Experimental Analysis of Behavior, 64(2), 117–128. doi:10.1901/jeab.1995.64-117
Simon, C. (2023). "You can be a behaviorist and still talk about the mind – as long as you don't put it into a person's head": An interview with Howard Rachlin. Journal of the Experimental Analysis of Behavior, VOLUME(ISSUE), PAGES.
Standing, L., Sproule, R., & Khouzam, N. (1991). Empirical statistics: IV. Illustrating Meehl's sixth law of soft psychology: Everything correlates with everything. Psychological Reports, 69(1), 123–126. doi:10.2466/PR0.69.5.123-126
Wagenmakers, E. J., Wetzels, R., Borsboom, D., & van der Maas, H. L. (2011). Why psychologists must change the way they analyze their data: The case of psi: Comment on Bem (2011). Journal of Personality and Social Psychology, 100(3), 426–432. doi:10.1037/a0022790
Xu, S., Pan, Y., Qu, Z., Fang, Z., Yang, Z., Yang, F., … Rao, H. (2018). Differential effects of real versus hypothetical monetary reward magnitude on risk-taking behavior and brain activity. Scientific Reports, 8. doi:10.1038/s41598-018-21820-0