XGBoost, missing values, and sparsity
Created 12 Sep 2018 • Last modified 18 Apr 2020
I use a simple example to describe how XGBoost handles missing data, and to demonstrate that sparse-matrix input can cause it to treat 0s as missing. (All code is in R.)
The good
Consider this dataset:
d = data.frame(
x = c(0, 1, NA),
y = c(4, 5, 99))
Let's use XGBoost to fit a single tree, with no regularization:
library(xgboost) m = xgboost( data = matrix(d$x), label = d$y, base_score = 0, gamma = 0, eta = 1, lambda = 0, nrounds = 1, objective = "reg:linear")
The model can perfectly reproduce its training data, including the case with x missing:
cbind(x = d$x, y.actual = d$y, y.pred = predict(m, matrix(d$x)))
| x | y.actual | y.pred | |
|---|---|---|---|
| 1 | 0 | 4 | 4 |
| 2 | 1 | 5 | 5 |
| 3 | 99 | 99 |
Here's what the tree looks like:
library(DiagrammeR) tree = xgb.plot.tree(model = m, render = F) export_graph(tree, "/tmp/tree.png", width=500, height=300)
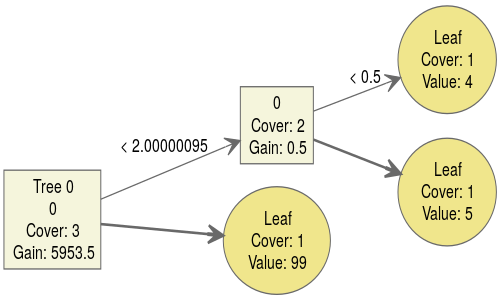
You can see how cases are routed through the tree according to the value of x (here called 0, since I didn't tell the xgboost function the name of the feature) when x = 0 or x = 1. When x is missing (NA), we use the so-called default direction to decide where a case goes when the tree is splitting on x. The default direction is indicated in the picture by the bold arrows. Thus we end up at the bottom leaf when x is missing.
How XGBoost finds and uses the default direction is described in section 3.4, "Sparsity-Aware Split Finding", of Chen and Guestrin (2016). I find the pseudocode somewhat cryptic, but the idea seems to be that the gain of both possible default directions is checked and the one that obtains better gain is used (and the default direction is optimized simultaneously with the feature to be split and the split point).
In the computation of SHapley Additive exPlanation (SHAP) values, predictors that have missing values don't need special treatment:
cbind(x = d$x, y.pred = predict(m, matrix(d$x)),
`colnames<-`(predict(m, matrix(d$x), predcontrib = T),
c("shap.x", "shap.bias")))
| x | y.pred | shap.x | shap.bias | |
|---|---|---|---|---|
| 1 | 0 | 4 | -32 | 36 |
| 2 | 1 | 5 | -31 | 36 |
| 3 | 99 | 63 | 36 |
The SHAPs for each case add up to the prediction (y.pred), and the overall SHAP bias is the mean of the predictions, so for a one-predictor model like this, the SHAP for the predictor is just the deviation from the mean prediction.
The bad
What's confusing about the aforementioned section of Chen and Guestrin (2016) is that the authors seems to conflate sparsity (a high occurrence of a single value, typically 0, and the use of special data structures and algorithms to exploit this property) with missing values (the lack of a known value for a given case and variable). In particular, Chen and Guestrin call missing values a cause of sparsity. How this seems to shake out is that when XGBoost is given a sparse matrix as input, it will treat 0s as if they were missing:
library(Matrix) ds = Matrix(matrix(d$x), sparse = T) cbind(x = d$x, y.actual = d$y, y.pred = predict(m, ds))
| x | y.actual | y.pred | |
|---|---|---|---|
| 1 | 0 | 4 | 99 |
| 2 | 1 | 5 | 5 |
| 3 | 99 | 99 |
The way this usually bites users of XGBoost is that they find that they get different overall results when they provide their data as a sparse matrix compared to a dense matrix (see e.g. here and here). XGboost has a missing parameter that from the documentation you might think could be set to NA to resolve this, but NA is in fact the default. Note also that training with a sparse matrix doesn't fix XGBoost's inability to distinguish sparse 0s from missing values:
M = Matrix(matrix(d$x), sparse = T) m2 = xgboost( data = M, label = d$y, base_score = 0, gamma = 0, eta = 1, lambda = 0, nrounds = 1, objective = "reg:linear") cbind(x = d$x, y.actual = d$y, y.pred = predict(m2, M))
| x | y.actual | y.pred | |
|---|---|---|---|
| 1 | 0.0 | 4.0 | 51.5 |
| 2 | 1.0 | 5.0 | 5.0 |
| 3 | 99.0 | 51.5 |
The number 51.5 appears here because it's the mean of 4 and 99.
So, I recommend only using dense matrices with XGBoost.
References
Chen, T., & Guestrin, C. (2016). XGBoost: A scalable tree boosting system. Retrieved from http://arxiv.org/abs/1603.02754